Вычислить указанные пределы не пользуясь правилом лопиталя.лучше с полным расписанием решения

Показать ответ

Ответ:

Куликова2006

22.06.2021 20:54

1. а) 2а + 3а = 5а;

б) 7х - 15х = -8x;

в) -17b - 3b = -20b;

г) -2,1y + 7y = 4,9y;

д) -2, 5х + х = -1,5x;

е) -а - 0,8а = -1,8а;

ж) 1/3 x - 2х = -1 2/3x;

з) 1/2а + 1/5а = 7/10а;

и) 5/6 - b = -1/6 b.

2. а) 85 + 12b - 21b + b = (8 + 12 - 21 + 1)b = 0 • b = 0;

б) —13с + 12с + 40с — 18с = (-13 + 12 + 40 - 18)с = 21с;

в) —р — р — р — 3р — р — р = (-1 - 1 - 1 - 3 - 1 - 1)р = —8р;

г) 4,14а + 8,73а + 5,8а — а = (4,14 + 8,73 + 5,8 - 1)а = 17,67а;

3. а) 10а — а — 6 + 76 = (10 - 1)а + (7 - 1)b = - 9а + 66;

б) —15с — 15а + 8а + 4с = (4 — 15)с + (8 — 15)а = -11 - 7а;

в) 0, 3х + 1,6у — 0, Зх — 0,4у = (0,3 — 0,3)х + (1,6- 0, 4)у = 0 + 1,2y = 1,2у;

г) х + у — х — у + 4 = (1 — 1)х + (1 — 1 )у + 4 = 0 + 0 + 4 = 4;

д) 5 — а +4а — b — 6а = 5 + (—1 + 4 — 6)а — b = 5 — За — 6;

е) 1,2с + 1 — 0,6у — 0,8 — 0,2с = (1,2 — 0,2)с — 0,6y + (1 — 0,8) = с - 0,6 + 0,2.

0,0(0 оценок)

Ответ:

Anna888Anna1

08.04.2021 21:33

Задание №1

а).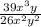 $\frac{39x^{3}y }{26x^{2} y^{2} }$ (сокращаем на "13 $x^{2}$ y")

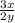
$\frac{3x}{2y}$

ответ: $\frac{3x}{2y}$

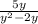б). $\frac{5y}{y^{2}-2y }$ (в знаменателе выносим "y" и сокращаем с "y" в числителе)

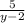
$\frac{5y}{y(y-2)} = \frac{5}{y-2}$

ответ: $\frac{5}{y-2}$

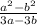в). $\frac{a^{2}-b^{2} }{3a-3b}$ (раскрываем числитель по формуле разности квадратов 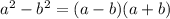$a^{2} -b^{2} = (a-b)(a+b)$ , в знаменателе выносим "3")

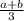
$\frac{(a-b)(a+b)}{3(a-b)} = \frac{a+b}{3}$

ответ: $\frac{a+b}{3}$

Задание №2

а).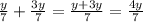 $\frac{y}{7}+\frac{3y}{7} = \frac{y+3y}{7} = \frac{4y}{7}$ (одинаковый знаменатель, значит можно складывать)

ответ: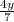 $\frac{4y}{7}$

б).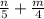 $\frac{n}{5}+\frac{m}{4}$ (знаменатели разные, чтобы сложить приводим к общему знаменателю. Первую дробь умножаем на 4, вторую умножаем на 5, после чего складываем)

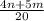
$\frac{n*4}{5*4}+\frac{m*5}{4*5}= \frac{4n}{20} +\frac{5m}{20} = \frac{4n+5m}{20}$

ответ: $\frac{4n+5m}{20}$

в). $\frac{3}{2a}-\frac{5}{3a}$ (принцип тот же. "а" есть и там, и там в знаменателе, значит первую дробь умножаем на 3, вторую умножаем на 2, чтобы получить общий знаменатель, после чего вычитаем)

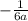
$\frac{3*3}{2a*3}-\frac{5*2}{3a*2} = \frac{9}{6a}-\frac{10}{6a} = -\frac{1}{6a}$

ответ: $-\frac{1}{6a}$

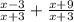г). $\frac{x-3}{x+3}+\frac{x+9}{x+3}$ (знаменатель одинаковый - складываем)

$\frac{x-3}{x+3}+\frac{x+9}{x+3} = \frac{x-3+x+9}{x+3}= \frac{2x+6}{x+3}=\frac{2(x+3)}{x+3} = 2$

ответ: 2

Задание №3

а).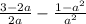 $\frac{3-2a}{2a} -\frac{1-a^{2} }{a^{2} }$ (умножаем первую дробь на a, а вторую умножаем на 2, после чего вычитаем дроби)

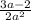
$\frac{3-2a}{2a} -\frac{1-a^{2} }{a^{2} } = \frac{(3-2a)*a}{2a*a}-\frac{(1-a^{2})*2}{a^{2}*2} = \frac{3a-2a^{2} }{2a^{2} } -\frac{2-2a^{2} }{2a^{2} } = \frac{3a-2a^{2}-2+2a^{2} }{2a^{2} } = \frac{3a-2}{2a^{2} }$

ответ: $\frac{3a-2}{2a^{2} }$

б). $\frac{1}{3x+y}-\frac{1}{3x-y}$ (первую дробь умножаем на знаменатель второй дроби, а вторую дробь умножаем на знаменатель первой дроби, после чего вычитаем)

$\frac{3x-y}{(3x+y)(3x-y)} -\frac{3x+y}{(3x-y)(3x+y)} = \frac{3x-y-3x-y}{(3x+y)(3x-y)}= \frac{-2y}{(3x+y)(3x-y)}$ (ещё можно свернуть по формуле разности квадратов $a^{2} -b^{2} = (a-b)(a+b)$ )

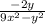
ответ: $\frac{-2y}{9x^{2}-y^{2} }$

в). $\frac{3}{b-2}-\frac{4-3b}{b^{2}-2b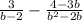}$ (вынесем "b" в знаменателе второй дроби за скобку и умножим первую дробь на "b", после чего вычитаем)

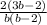
$\frac{3*b}{(b-2)*b}-\frac{4-3b}{b(b-2)} = \frac{3b}{b(b-2)} -\frac{4-3b}{b(b-2)} = \frac{3b-4+3b}{b(b-2)} = \frac{6b-4}{b(b-2)} = \frac{2(3b-2)}{b(b-2)}$

ответ: $\frac{2(3b-2)}{b(b-2)}$

Задание №4

$\frac{x-6y^{2} }{2y} +3y$ (приведем к общему знаменателю умножив $\frac{3y}{1}$ на "2y", после чего сложим)

$\frac{x-6y^{2} }{2y} +\frac{3y*2y}{2y} = \frac{x-6y^{2} }{2y} + \frac{6y^{2} }{2y} = \frac{x-6y^{2}+6y^{2} }{2y} = \frac{x}{2y}$ (теперь подставляем x = -8 и y = 0,1. Десятичное число 0,2 = дроби $\frac{2}{10}$ . Когда получилась трёхэтажная дробь, то знаменатель дроби в знаменателе переносится в числитель и умножается на числитель общей дроби, а знаменатель становится числитель дроби в знаменателе)

$\frac{x}{2y} = \frac{-8}{2*0,1}= \frac{-8}{0,2}= \frac{-8}{\frac{2}{10} } = \frac{-8*10}{2} = \frac{-80}{2} = -40$

ответ: -40

Задание №5

$\frac{2}{x-4}-\frac{x+8}{x^{2}-16} -\frac{1}{x}$ (знаменатель средней дроби раскроем по формуле разности квадратов $a^{2} -b^{2} = (a-b)(a+b)$ .

Первую дробь умножим на "х" и на "x+4", среднюю дробь умножим на "х", а третью дробь умножим на "x+4" и на "x-4", после чего посчитаем)

$\frac{2*x*(x+4)}{(x-4)*x*(x+4)}-\frac{(x+8)*x}{(x-4)(x+4)*x} -\frac{(x-4)(x+4)}{x(x-4)(x+4)} = \frac{2x^{2}+8x}{x(x-4)(x+4)}-\frac{x^{2}+8x}{x(x-4)(x+4)}-\frac{x^{2}-16}{x(x-4)(x+4)} =\frac{2x^{2}+8x-x^{2}-8x-x^{2}+16}{x(x-4)(x+4)} =\frac{16}{x(x-4)(x+4)} = \frac{16}{x(x^{2}-16)} = \frac{16}{x^{3}-16x}$ ответ: $\frac{16}{x^{3}-16x}$