По условию, выражение -5с-с² принимает отрицательные значения, т.е. значения меньше нуля. Таким образом, задача сводится к решению неравенства -5с-с²<0 Решение: -5c-c²<0 (умножаем обе части неравенства на (-1), при этом знак меняется) c²+5c>0 (разложим на множители левую часть неравенства) c(c+5)>0 (далее решаем методом интервалов) + - + (-5)(0)
Т.к. знак неравенства > (больше нуля), то выбираем области, где стоит знак плюс, получаем ответ: с∈(-∞;-5)U(0;+∞)
Решение:
-5c-c²<0 (умножаем обе части неравенства на (-1),
при этом знак меняется)
c²+5c>0 (разложим на множители левую часть неравенства)
c(c+5)>0 (далее решаем методом интервалов)
+ - +
(-5)(0)
Т.к. знак неравенства > (больше нуля), то выбираем области, где стоит знак плюс, получаем ответ:
с∈(-∞;-5)U(0;+∞)
Доказательство:
Дана последовательность
Допустим, что эта последовательность арифметическая прогрессия, тогда
при n = 1 получаем
при n = 2
и
а₂ = -2 - а₁ = -2 + 2 = 0
Таким образом разность арифметической прогрессии
d = a₂ - a₁ = 0 + 2 = 2
По известной формуле найдем n-й член арифметической прогрессии
Известно, что сумма n членов арифметической прогрессии
Докажем, что выражение (2) тождественно выражению (1) при
a₁ = -2 и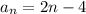
, подставив в (2)
Тождество доказано.
Следовательно, последовательность, определённая суммой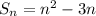
является арифметической прогрессией.