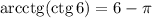График функции y=-3х это прямая с угловым коэффициентом к = -3. У параллельной прямой угловой коэффициент равен этому значению. Чтобы построить график, который проходит через точку (0;4) и параллелен графику функции y=-3х надо подставить координаты заданной точки в уравнение у = -3х + в. 4 = -3*0 + в. Отсюда в = 4. Тогда получаем уравнение у = -3х + 4.
Можно было рассуждать несколько иначе. В уравнении прямой с угловым коэффициентом вида у = кх + в параметр в обозначает координату точки пересечения прямой оси Оу. Так как в задании дана точка (0; 4) - то она лежит на оси Оу и координата по оси Оу и является является величиной в. Можно было сразу записать уравнение у = -3х + 4.
Кроме этого, известно, что основной период котангенса равен :
Таким образом, аргумент 6 нужно заменить некоторым аргументом вида , чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
Запишем неравенство:
Выполним оценку обеих частей неравенства:
Получим:
Или записывая соотношение для k:
Единственное подходящее целое значение: .
Запишем:
Действительно, , арккотангенс может принимать такое значение.
У параллельной прямой угловой коэффициент равен этому значению.
Чтобы построить график, который проходит через точку (0;4) и параллелен графику функции y=-3х надо подставить координаты заданной точки в уравнение у = -3х + в.
4 = -3*0 + в.
Отсюда в = 4.
Тогда получаем уравнение у = -3х + 4.
Можно было рассуждать несколько иначе.
В уравнении прямой с угловым коэффициентом вида у = кх + в параметр в обозначает координату точки пересечения прямой оси Оу.
Так как в задании дана точка (0; 4) - то она лежит на оси Оу и координата по оси Оу и является является величиной в.
Можно было сразу записать уравнение у = -3х + 4.
Известно соотношение:
Кроме этого, известно, что основной период котангенса равен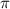 :
:
Таким образом, аргумент 6 нужно заменить некоторым аргументом вида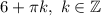 , чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
, чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
Запишем неравенство:
Выполним оценку обеих частей неравенства:
Получим:
Или записывая соотношение для k:
Единственное подходящее целое значение: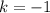 .
.
Запишем:
Действительно, , арккотангенс может принимать такое значение.
, арккотангенс может принимать такое значение.
ответ: