Имеем
Используя выражение
преобразуем запись в
Используем и упрощаем наше выражение и получаем ответ
Имеем
Используя выражение
преобразуем запись в
Используем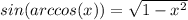 и
и 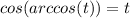 упрощаем наше выражение и получаем ответ
упрощаем наше выражение и получаем ответ