Чтобы доказать, что отрезок BD является медианой треугольника и определить длину отрезка AD, мы будем использовать информацию о равенстве треугольников.
Дано: Равнобедренный треугольник ABC, где AB = BC = 55 cm. Биссектриса угла ∠ABC проведена и пересекает сторону AC в точке D.
Доказательство:
Шаг 1: По условию задачи, у нас есть следующие равенства углов:
∠A = ∠C (потому что у равнобедренного треугольника прилежащие к основанию углы равны).
Шаг 2: Мы также знаем, что биссектриса делит угол ∠ABC пополам, поэтому у нас есть равенство углов:
∠DBA = ∠DBC.
Шаг 3: Следующий шаг - сравнить стороны треугольников ΔABD и ΔCBD. Мы знаем, что AB = BC, так как это равнобедренный треугольник.
Шаг 4: Согласно второму признаку равенства треугольников, если у двух треугольников равны две стороны и угол между ними, то они равны. В нашем случае, у треугольников ΔABD и ΔCBD равны стороны AB и BC, а также угол ∠DBA = ∠DBC.
Исходя из этого признака, мы можем сделать вывод, что все соответствующие элементы треугольников равны, включая стороны AD и CD.
Шаг 5: Значит, AD = CD и отрезок BD является медианой треугольника ΔABC, так как медиана делит сторону AC пополам.
Теперь, чтобы определить длину отрезка AD, нам нужно знать длину стороны AC.
Длина стороны AC может быть найдена из равенства сторон треугольника ΔABC: AB = BC = 55 см.
Так как треугольник ABC равнобедренный, стороны AC и BC равны. Следовательно, длина стороны AC также равна 55 см.
Таким образом, длина отрезка AD равна половине длины стороны AC, то есть AD = AC/2. В нашем случае, AD = 55/2 = 27.5 см.
Итак, мы доказали, что отрезок BD является медианой треугольника, а длина отрезка AD равна 27.5 см.
Теперь, когда у нас есть новые координаты, мы можем построить график функции `y=-f(x)`.
3) Функция `y=-1/3f(x)`:
- В этой функции нужно изменить значения функции `f(x)`. Это означает, что каждая точка графика `f(x)` должна быть изменена по вертикальной оси, поделенная на 3.
Чтобы получить новый график функции `y=-1/3f(x)`, нужно взять точки исходного графика `f(x)` и поделить их ординаты на 3.
Давайте применим этот подход к нашему рисунку:
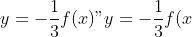")
Дано: Равнобедренный треугольник ABC, где AB = BC = 55 cm. Биссектриса угла ∠ABC проведена и пересекает сторону AC в точке D.
Доказательство:
Шаг 1: По условию задачи, у нас есть следующие равенства углов:
∠A = ∠C (потому что у равнобедренного треугольника прилежащие к основанию углы равны).
Шаг 2: Мы также знаем, что биссектриса делит угол ∠ABC пополам, поэтому у нас есть равенство углов:
∠DBA = ∠DBC.
Шаг 3: Следующий шаг - сравнить стороны треугольников ΔABD и ΔCBD. Мы знаем, что AB = BC, так как это равнобедренный треугольник.
Шаг 4: Согласно второму признаку равенства треугольников, если у двух треугольников равны две стороны и угол между ними, то они равны. В нашем случае, у треугольников ΔABD и ΔCBD равны стороны AB и BC, а также угол ∠DBA = ∠DBC.
Исходя из этого признака, мы можем сделать вывод, что все соответствующие элементы треугольников равны, включая стороны AD и CD.
Шаг 5: Значит, AD = CD и отрезок BD является медианой треугольника ΔABC, так как медиана делит сторону AC пополам.
Теперь, чтобы определить длину отрезка AD, нам нужно знать длину стороны AC.
Длина стороны AC может быть найдена из равенства сторон треугольника ΔABC: AB = BC = 55 см.
Так как треугольник ABC равнобедренный, стороны AC и BC равны. Следовательно, длина стороны AC также равна 55 см.
Таким образом, длина отрезка AD равна половине длины стороны AC, то есть AD = AC/2. В нашем случае, AD = 55/2 = 27.5 см.
Итак, мы доказали, что отрезок BD является медианой треугольника, а длина отрезка AD равна 27.5 см.
1) Функция `y=2f(x)`:
- В этой функции нужно умножить значения функции `f(x)` на 2. Это означает, что каждая точка графика `f(x)` должна быть удвоена по вертикальной оси.
Чтобы получить новый график функции `y=2f(x)`, нужно взять точки исходного графика `f(x)` и умножить их ординаты на 2.
Давайте применим этот подход к нашему рисунку:
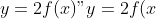")
Таким образом, каждая точка исходного графика умножается на 2:
- Координаты A: `(1,2)`
- Координаты B: `(2,4)`
- Координаты C: `(3,-2)`
- Координаты D: `(4,-6)`
- Координаты E: `(6,2)`
Теперь, когда у нас есть новые координаты, мы можем построить график функции `y=2f(x)`.
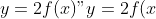")
2) Функция `y=-f(x)`:
- В этой функции нужно изменить знак функции `f(x)`. Это значит, что значения функции `f(x)` должны быть умножены на -1.
Чтобы получить новый график функции `y=-f(x)`, нужно взять точки исходного графика `f(x)` и изменить их ординаты на противоположные.
Давайте применим этот подход к нашему рисунку:
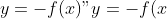")
Таким образом каждая y-координата отражается и помещается в противоположную сторону:
- Координаты A: `(1,-2)`
- Координаты B: `(2,-4)`
- Координаты C: `(3,2)`
- Координаты D: `(4,6)`
- Координаты E: `(6,-2)`
Теперь, когда у нас есть новые координаты, мы можем построить график функции `y=-f(x)`.
3) Функция `y=-1/3f(x)`:
- В этой функции нужно изменить значения функции `f(x)`. Это означает, что каждая точка графика `f(x)` должна быть изменена по вертикальной оси, поделенная на 3.
Чтобы получить новый график функции `y=-1/3f(x)`, нужно взять точки исходного графика `f(x)` и поделить их ординаты на 3.
Давайте применим этот подход к нашему рисунку:
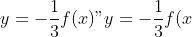")
Таким образом каждая y-координата делится на 3:
- Координаты A: `(1,-2/3)`
- Координаты B: `(2,-4/3)`
- Координаты C: `(3,2/3)`
- Координаты D: `(4,2)`
- Координаты E: `(6,-2/3)`
Теперь, когда у нас есть новые координаты, мы можем построить график функции `y=-1/3f(x)`.
Это объяснение и пошаговое решение помогут школьнику лучше понять, как построить каждый график и что означают данные изменения функций.