Уравнение. Правая часть - это ноль. Значит с лева, тоже имеем ноль. Как это может быть? 1. (y-3)=0 или (5+2y)=0 и (5-2y)=0 2. (y-3)(5+2y) = (5-2y)(5-2y)
Рассмотрим случай №1 y=3 или y=-2,5 и y=2,5 - переменная y не может иметь сразу 2 разных числовых значения, этот случай отпадает, а жаль.
Придется рассмотреть случай №2 (раскрыть скобки, упростить, получить квадратное уравнение, решить его, проверить корни). (y-3)(5+2y) = (5-2y)(5-2y) 5y+2yy-15-6y = 25-10y-10y+4yy 4yy-20y+25-2yy+1y+15 = 0 2yy-19y+40 = 0 a = 2 b = -19 c = 40 sqr - квадратный корень, пример записи sqr(4) = 2.
x1=(-b+sqr(bb-4ac))/2a = (19+sqr(19*19-4*2*40))/2*2 = (19+sqr(361-320))/4 Примерно x1 = (19+6,4)/4 = 6,35 Проблемы с тем, что корень из 41 число не целое. x2=(-b-sqr(bb-4ac))/2a = (19-sqr(19*19-4*2*40))/2*2 = (19-sqr(361-320))/4 Примерно x2 = (19-6,4)/4 = 12,6/4 = 3,15
2yy-19y+40 = 0 При x1 = 6,35 80.645-120.65+40 = 120.645 - 120.65 = примерно ноль При x2 = 3,15 19.845-59.85+40 = 59.845-59.85 = примерно ноль ответ: x1 = 6,35; x2 = 3,15.
См. рисунок
1. Правильный шестиугольник, состоит из шести равносторонних треугольников.
Найдем сторону шестиугольника AB=r=48/6=8м.
Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD
По теореме Пифагора найдем СD
r²=CD²+DO²=2CD² ⇒ r=CD√2⇒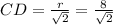 м
м
2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.
Площадь правильного шестиугольника равна
Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см
3. Площадь сектора равна
(где n - градусная мера дуги сектора)
1. (y-3)=0 или (5+2y)=0 и (5-2y)=0
2. (y-3)(5+2y) = (5-2y)(5-2y)
Рассмотрим случай №1
y=3 или y=-2,5 и y=2,5 - переменная y не может иметь сразу 2 разных числовых значения, этот случай отпадает, а жаль.
Придется рассмотреть случай №2 (раскрыть скобки, упростить, получить квадратное уравнение, решить его, проверить корни).
(y-3)(5+2y) = (5-2y)(5-2y)
5y+2yy-15-6y = 25-10y-10y+4yy
4yy-20y+25-2yy+1y+15 = 0
2yy-19y+40 = 0
a = 2
b = -19
c = 40
sqr - квадратный корень, пример записи sqr(4) = 2.
x1=(-b+sqr(bb-4ac))/2a = (19+sqr(19*19-4*2*40))/2*2 = (19+sqr(361-320))/4
Примерно x1 = (19+6,4)/4 = 6,35
Проблемы с тем, что корень из 41 число не целое.
x2=(-b-sqr(bb-4ac))/2a = (19-sqr(19*19-4*2*40))/2*2 = (19-sqr(361-320))/4
Примерно x2 = (19-6,4)/4 = 12,6/4 = 3,15
2yy-19y+40 = 0
При x1 = 6,35
80.645-120.65+40 = 120.645 - 120.65 = примерно ноль
При x2 = 3,15
19.845-59.85+40 = 59.845-59.85 = примерно ноль
ответ: x1 = 6,35; x2 = 3,15.