найдем точки пересечения
x+2=0
x=-2
теперь между 2 и -2 лежать 0 значит интеграруем от -2 до 2
Площадь фигуры ограниченной двумя функциями вычисляется по формуле:
Так как функция пересает ось абсцисс в точке -2, получаем границы интегрирования:
ответ:S=8
найдем точки пересечения
x+2=0
x=-2
теперь между 2 и -2 лежать 0 значит интеграруем от -2 до 2
Площадь фигуры ограниченной двумя функциями вычисляется по формуле:
Так как функция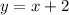
пересает ось абсцисс в точке -2, получаем границы интегрирования:
ответ:S=8