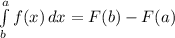343/6≈51.167
Объяснение:
Начертим график для параболы. Из него видно, что она располагается в пределах от 0 до 7 . В этих пределах мы и будем интегрировать функцию.
Подставляем пределы по формуле Ньютона-Лейбница:
343/6≈51.167
Объяснение:
Начертим график для параболы. Из него видно, что она располагается в пределах от 0 до 7 . В этих пределах мы и будем интегрировать функцию.
Подставляем пределы по формуле Ньютона-Лейбница: