Вычислите пределы: 1.lim x→a 3x^2−48/(x−3)(x^2−8x+16), если a) a=0; б) a=+∞; в) a=−4. В ответе указать сумму всех пределов. 2.Пользуясь замечательным показательно-степенным пределом, вычислите lim x→0 (cos2x)^1/sin4x. 3.Выделить целую часть рациональной функции 2x^4+3x^3+2x^2−5/x^2+1
ответ: x=7/4
Объяснение:
√(3x+1)/x + 4*(√(3x+1)/3 -√(4x-3) ) = 13/3 - 4x -1/x
ОДЗ : x>=3/4
Поскольку x≠0 , умножим обе части уравнения на 3x :
3*√(3x+1) +4x*√(3x+1) -12*x*√(4x-3) = -12*x^2+13*x-3
√(3x+1)*(4x+3) -12*x*√(4x-3) +12*x^2 -13*x +3 = 0
√(3x+1)*(4x+3) +(12*x^2 -9x - 12*x*√(4x-3) +12*x) -16*x+3=0
Заметим, что :
12*x^2 -9x - 12*x*√(4x-3) +12*x = 3*x*( 4x-3 -4*x*√(4x-3) +4) =
=3*x*( √(4x-3) -2 )^2
√(3x+1)*(4x+3) -16*x +3 + 3*x*( √(4x-3) -2 )^2 = 0
Разложим отдельно выражение:
√(3x+1)*(4x+3) -16*x +3 =
=√(3x+1)*(4x+3) +4x +3 -20*x = (√(3x+1) +1)*(4x+3)-20*x
Заметим, что 3x = (√(3x+1) )^2 - 1 = (√(3x+1) -1)*(√(3x+1) +1)
(√(3x+1) +1)*(4x+3)-20*x =
=(√(3x+1) +1)*(4x+3) -20/3 *(√(3x+1) -1)*(√(3x+1) +1) =
=(√(3x+1) +1)*(4x+3-20/3 *(√(3x+1) -1) ) =
=1/3 * (√(3x+1) +1)*(12x+9-20*√(3x+1) +20 )
Упростим отдельно:
12x+9-20*√(3x+1) +20 = 12x+4 -20*√(3x+1) +25 = (2*√(3x+1) -5)^2
1/3 * (√(3x+1) +1)*(12x+9-20*√(3x+1) +20 ) =
=1/3 *(√(3x+1) +1)*(2*√(3x+1) -5)^2
Таким образом, уравнение принимает вид :
1/3 *(√(3x+1) +1)*(2*√(3x+1) -5)^2 + 3*x*( √(4x-3) -2 )^2 = 0
Поскольку радикал положителен, то
1) 1/3 *(√(3x+1) +1)*(2*√(3x+1) -5)^2 >=0
Поскольку x>=3/4 >0
2) 3*x*( √(4x-3) -2 )^2 >=0
Но тогда сумма выражений 1) и 2) может быть равна 0, только когда оба выражения 1) и 2) одновременно равны 0.
1) 3*x*( √(4x-3) -2 )^2 = 0
x≠0
√(4x-3) -2 = 0
√(4x-3) = 2
4x-3 =4
x=7/4 > 3/4
2) (√(3x+1) +1)*(2*√(3x+1) -5)^2 =0
√(3x+1) +1 =0
√(3x+1) =-1 ( нет решений)
2*√(3x+1) -5 = 0
2*√(3x+1) = 5
4*(3x+1) =25
12x+4=25
12x=21
x=21/12 = 7/4
Таким образом, корень совпадает, а значит уравнение имеет единственное решение : x=7/4
a) 4
б) [0, 4] и [4, +∞]
в) убывает на [0, +∞)
г) (-∞, 1)
Объяснение:
Строим график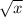
График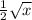
Является сплюснутой в два раза по оси y версией графика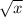
Отзеркаливаем его относительно оси x и получаем график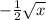
Чтобы получить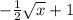
Надо поднять график 
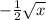вверх по оси y на 1 единицу.
График построен (смотри картинку).
a) Нули функции - x при котором функция равна нулю. Это 4.
б) Промежутки знакопостоянства - промежутки, на которых функция сохраняет свой знак. Это [0, 4] и [4, +∞)
в) Промежутки возрастания и убывания функции. Убывает на [0, +∞)
г) Область значений функции - множество всех значений функции, которые она принимает при переборе всех x из области определения
(-∞, 1)
============
Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!