Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Х
Химия
Д
Другие предметы
Н
Немецкий язык
Б
Беларуская мова
М
Музыка
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
У
Українська література
Р
Русский язык
Ф
Французский язык
П
Психология
О
Обществознание
А
Алгебра
М
МХК
Г
География
И
Информатика
П
Право
А
Английский язык
Г
Геометрия
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
dinkooo96
03.01.2021 03:11 •
Алгебра
Вычислите sin^3 15°+cos^3 15°
Показать ответ
Ответ:
persik2113
17.06.2021 23:03
ответ:
.
0,0
(0 оценок)
Популярные вопросы: Алгебра
DALERALIMOV02
09.03.2021 01:32
Решение с рациональных уравнений первую половину пути поезд со скоростью 50 км/ч, а затем увеличил скорость. какой была скорость поезда во второй половине пути, если известно, что...
kovalcuk
26.12.2020 04:31
Розвяжіть систему рівнянь 3xy+x=8 3xy+y=7...
лизанезнающая
26.12.2020 04:31
Постройте график функции. y=(x-3)²-2. определите промежутки возрастания и убывания функции....
1321321325555555
13.11.2020 15:55
При взвешивании купленного винограда получилось 6,6 кг, причем известно, что предельная абсолютная погрешность равна 33г. определите предельную относительную погрешность и границы...
дуажрлвдаддвдабдв
26.12.2020 04:31
Выполните умножение одночлена на многочлен : а) 3b(x-4) б) -a(x+y) в) -2a(x-3y+5) г) 6b(-b+y во второй степени -3)...
p111111197
26.12.2020 04:31
Решить пример. (-1,2) во 2 степени умножить на (1/3) в третьей степени. пришлите полное решение...
andreykolomoytsev
24.06.2021 02:39
Выполните вычитание: c^2/c^2-16-c/c+4...
Giga45
04.01.2021 22:06
Постройте график уравнения 2х+y=3. с фото....
nasamar
04.01.2021 22:06
Judy: i don t think that photography is a boring hobby. i find it very interesting.перевод ....
евгения406
12.10.2021 22:20
Самостійна робота з алгебри 9 клас,дуже ❤...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
ответ: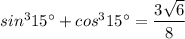 .
.