х ≠ 0 , но этот разрыв производной нас не интересует, поскольку мы ищем наибольшее значение в интервале [1; 16]
y' = 0
(27 - 3x) = 0
Точка экстремума одна x = 9.
При х < 9 y' > 0; при х > 9 y' < 0. Следовательно, точка х = 9 - точка максимума. И на концах интервала при непрерывной производной в заданном интервале значения функции будут меньше её значения в точке локального максимума.
Этот ряд чисел образует арифметическую прогрессию, т.е. последовательность чисел, каждый член которой, начиная со 2-го, равен предыдущему, сложенному с одним и тем же числом, называемым разностью прогрессии - это число 5.
Имеем: а₁ = 10, разность d = 5.
Найдем номер последнего члена прогрессии, равного 95:
an = a₁₁ + d(n - 1) - формула n-го члена
95 = 10 + 5(n - 1),
10 + 5n - 5 = 95,
5 + 5n = 95,
5n = 95 - 5,
5n = 90,
n = 90 : 5,
n = 18.
Значит, всего двузначных чисел, кратных числу 5, - 18 штук.
Найдем S₁₈.
Sn = (a₁ + a₁₈)/2 · n - формула суммы n первых членов арифметической прогрессии
y наиб = у max = 54
Объяснение:
Дана функция y= (27 - x) · √x
Производная этой функции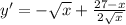
Упростим это выражение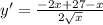
х ≠ 0 , но этот разрыв производной нас не интересует, поскольку мы ищем наибольшее значение в интервале [1; 16]
y' = 0
(27 - 3x) = 0
Точка экстремума одна x = 9.
При х < 9 y' > 0; при х > 9 y' < 0. Следовательно, точка х = 9 - точка максимума. И на концах интервала при непрерывной производной в заданном интервале значения функции будут меньше её значения в точке локального максимума.
у наиб = у max = y(9) = (27 - 9) · √ 9 = 54
Нужно найти сумму чисел: 10 + 15 + 20 + ... + 95.
Этот ряд чисел образует арифметическую прогрессию, т.е. последовательность чисел, каждый член которой, начиная со 2-го, равен предыдущему, сложенному с одним и тем же числом, называемым разностью прогрессии - это число 5.
Имеем: а₁ = 10, разность d = 5.
Найдем номер последнего члена прогрессии, равного 95:
an = a₁₁ + d(n - 1) - формула n-го члена
95 = 10 + 5(n - 1),
10 + 5n - 5 = 95,
5 + 5n = 95,
5n = 95 - 5,
5n = 90,
n = 90 : 5,
n = 18.
Значит, всего двузначных чисел, кратных числу 5, - 18 штук.
Найдем S₁₈.
Sn = (a₁ + a₁₈)/2 · n - формула суммы n первых членов арифметической прогрессии
S₁₈ = (10 + 95)/2 · 18 = 105 · 9 = 945.
ответ: 945.