выразим из каждого уравнения х, и приравняем полученное.
х=-2у-4 (1)
х=-7у+1 (2)
-2у-4=-7у+1⇒5у=5⇒у=5/5;у=1; подставим у=1 в любое из выражений (1)или (2) для определения х, получим х=-2*1-4=-6. Окончательно, найдена точка пересечения (-6;1)
Проверка. проверим решение для первого уравнения. подставив полученную точку, -6+2*1+4=0;0=0; и для второго исходного уравнения -6+7*1-1=0; 0=0.
Задание выполнено верно.
ответ координаты точки пересечения прямых
х=-6;у=1
РS : можно было из первых двух уравнений сначала выразить у, решить относительно х уравнение и найти все ту же точку (-6;1), но более рациональнее первое решение.
Можно было решить и третьим . Графически. Но, как правило, проще здесь первым .
Область , задающая плоскую фигуру, координаты центра тяжести которого требуется найти, задана такими кривыми:
Известны ограничения сверху и снизу на , а для только сверху. Тогда ограничение снизу будет граничным с остальными:
Получили четвёртое и последнее ограничение для области. Тогда область задана такими кривыми:
Переведём условия в вид неравенств:
Поскольку левые части неравенств области нулевые, можем сразу вычислить площадь области, не используя двойной интеграл, а вместо него использовав одномерный определённый интеграл, в качестве функции использовав верхний предел , а в качестве пределов интегрирования — части неравенства для .
Как известно, если — точка центра тяжести, то , и они в свою очередь:
выразим из каждого уравнения х, и приравняем полученное.
х=-2у-4 (1)
х=-7у+1 (2)
-2у-4=-7у+1⇒5у=5⇒у=5/5;у=1; подставим у=1 в любое из выражений (1)или (2) для определения х, получим х=-2*1-4=-6. Окончательно, найдена точка пересечения (-6;1)
Проверка. проверим решение для первого уравнения. подставив полученную точку, -6+2*1+4=0;0=0; и для второго исходного уравнения -6+7*1-1=0; 0=0.
Задание выполнено верно.
ответ координаты точки пересечения прямых
х=-6;у=1
РS : можно было из первых двух уравнений сначала выразить у, решить относительно х уравнение и найти все ту же точку (-6;1), но более рациональнее первое решение.
Можно было решить и третьим . Графически. Но, как правило, проще здесь первым .
Удачи.
Объяснение:
Область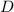 , задающая плоскую фигуру, координаты центра тяжести которого требуется найти, задана такими кривыми:
, задающая плоскую фигуру, координаты центра тяжести которого требуется найти, задана такими кривыми:
Известны ограничения сверху и снизу на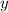 , а для
, а для  только сверху. Тогда ограничение снизу будет граничным с остальными:
только сверху. Тогда ограничение снизу будет граничным с остальными:
Получили четвёртое и последнее ограничение для области. Тогда область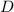 задана такими кривыми:
задана такими кривыми:
Переведём условия в вид неравенств:
Поскольку левые части неравенств области нулевые, можем сразу вычислить площадь области, не используя двойной интеграл, а вместо него использовав одномерный определённый интеграл, в качестве функции использовав верхний предел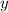 , а в качестве пределов интегрирования — части неравенства для
, а в качестве пределов интегрирования — части неравенства для  .
.
Как известно, если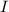 — точка центра тяжести, то
— точка центра тяжести, то 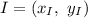 , и они в свою очередь:
, и они в свою очередь:
Найдём обе координаты точки центра тяжести.
Начнём с абсциссы:
Теперь ордината:
ответом будут найденные координаты,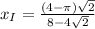 и
и 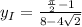 .
.