Вынеси общий множитель за скобки:
3m(m+n)−9n(m+n).
Определи общий множитель выражения d+b+c(d+b).
Разложи на множители x3+9x2−7x−63.
(Знаки + и − вводи в отдельные окошечки.)
Разложи на множители:
56am+21mu−24au−49m2.
Разложи на множители:
uz6+uy6−yz6−y7.
Вынеси общий множитель за скобки:
0,3t(t4+g)−0,8g(t4+g).
Сдвиг по фазе -30 градусов означает сдвиг всей кривой вправо на 1/6 полупериода или 1/12 периода (это чуть больше 0,5). отложите метки на оси.
Коэффициент 2 растягивает результат по вертикали симметрично, а сдвиг -1 сдвигает вниз на 1.
Окончательно кривая лежит между горизонталями +1 и -3
Реально надо бы рассчитать точку сдвига, помеченную крестом, и относительно неё строить с обычным периодом растянутую по вертикали косинусоиду.
Этот процесс нужно только для понимания как строится такая кривая.
А практически, вычисляем таблицу по формуле с малым шагом, откладываем точки на графике и соединяем плавно.
кубическая функция может иметь только локальный минимум. Потому что при х ->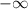
она уходит в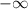 
точки минимума и максимума соответствуют нулям производной
сумма степеней равна нулю, значит один корень = 1, второй = a
локальным минимумом является больший корень (кубическая функция возрастает от минус бесконечности до первого корня, потом убывает, потом снова возрастает до плюс бесконечности)
значит при a<1 локальный минимум f(x=1) = 1/3 - (a+1)/2 + a - 7 = a/2 - 7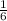
при а>1 локальный минимум f(x=a) = a^3/3-(a+1)/2*a^2+a^2 - 7 = (1/3 - 1/2) a^3 + (-1/2+1) a^2 - 7 = - a^3 / 6 + a^2 / 2 - 7
при a = 1 имеем точку перегиба и никакого минимума