Вынеси общий множитель за скобки: −60zx+75zy+105z. ответ:

−
(
x−
y
)

Сократи дробь 16−t24−t.

Выбери правильный ответ:
16−t3
4−t21−t
4+t
другой ответ
4−t

Разложи на множители 1−g2+2gh−h2.

Выбери правильный ответ:
(1−g)⋅(1+g+2h)
(1−g)⋅(1+h)
(g+h)2
(1−g+h)⋅(1+g−h)
(g−h)2

Найди значение выражения
4(k−10)−t(10−k), если k=2, t=6.

Числовое значение выражения равно

Разложи на множители:
2t4z2−16tz5.

Выбери правильный ответ:
2tz2⋅(t−2z)⋅(t+2z)
другой ответ
2tz2⋅(t−2z)⋅(t2+2tz+4z2)
2tz2⋅(t+2z)⋅(t2−2tz+4z2)
2tz2⋅(t−2z)⋅(t2+4tz+4z2)

Реши уравнение:
13y2+39y−(y+3)=0.

Корни уравнения
y1=
;y2=

Реши уравнение:
(9x−2)2−(x−16)2=0.

ответ:
x1=
;x2=

Реши уравнение 64g+64−g3−g2=0.

g1=
;g2=
;g3=
.

8

Объяснение:

Сложим два равенства, получим уравнение:

Раскроем скобки справа, перенесем влево и дополним до полных квадратов относительно х и у:

Выражаем x через y:

(вообще, правильнее было бы рассмотреть два случая: когда перед корнем стоит знак плюс, что мы и делаем, и когда перед ним стоит знак минус, но нас интересует максимальное значение, логичнее было бы рассмотреть только положительное значение)

Наша целевая функция, в которой будем находить максимум, имеет вид:

, где S - сумма решений системы уравнений.

Найдем производную по х, приравняем к нулю эту функцию

Получим

Таким образом, мы сможем найти y: y₁ = 4; y₂ = 4

Стало быть, только в точке (4;4) достигается этот максимум суммы, которая равна 4+4 = 8

В обоих случаях рассматриваем прямоугольный треугольник с одним из углов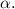

В первом случае примем прилежащий к углу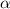  катет за 3, а гипотенузу - за 5. Тогда неизвестный катет вычислим по т. Пифагора как 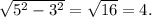Синус угла 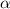есть отношение противолежащего катета к гипотенузе, т.е. 4/5. Тангенсом - отношение противолежащего катета к прилежащему, т.е. 4/3. Котангенсом - отношение прилежащего катета к противолежащему, т.е. 3/4.

Во втором случае примем катет, лежащий против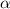 за 4, а гипотенузу - за 5. Неизвестный катет, по теореме Пифагора, будет равен 3. Косинусом 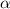есть отношение прилежащего катета к гипотенузе, т.е. 3/5. Тангенсом - отношение противолежащего катета к прилежащему, т.е. 4/3. Котангенсом - отношение прилежащего катета к противолежащему, т.е. 3/4.