вынести множитель из под корня :корень из 2^5*3^3
Корень а^3
Корень 16х^5

Объяснение:

Данная функция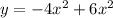 является квадратичной функцией (многочлен второй степени) и задаёт квадратичную параболу. Как известно, у такой функции может быть лишь один экстремум, находящийся в вершине параболы.

Упростим исходную функцию: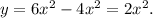

Для нахождения единственного экстремума воспользуемся производной:

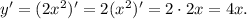
По лемме Ферма, значение производной от экстремума нулевое. Таким образом, точки экстремума будет решением .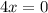

Для нахождения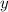 точки экстремума вычислим значение исходной функции от найденного :

Получается, что координаты точки экстремума это .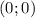

Объяснение:

x²-36=0;

x²=36;

x=±6.

***

2x²-3x=0;

x(2x-3)=0;

x1=0;

2x=3;

x=3/2;

x2=1.5.

***

4x²-x=3x-1;

4x²-4x+1=0;

a=4;  b=-4;  c=1;

D=b²-4ac=(-4)²-4*4*1=16-16=0 - два равных корня.

х1=x2=(-b)/2a=(-(-4))/2*4=4/8=1/2=0.5.

***

6x²+9x-2x-3=6x-3;

6x²+x=0;

x(6x+1)=0;

x1=0;

6x=-1;

x2= - 1/6.

***

12x+18-2x²-12x-12=0;

-2x²+6=0;

x²=3;

x1,2=±√3

***

(3x-1)² - (x+2)²=15;

9x²-6x+1 - x²-4x-4-15=0;

8x²-10x-18=0; [: 2]

4x²-5x-9=0;

a=4;  b=-5;  c=-9;

D=b²-4ac=(-5)²-4*4*(-9)=25+144=169=13² >0  0  -  два корня.

x1=(-b+√D)/2a=(-(-5)+13)/2*4=(5+13)/8 =18/8=2.25;

x2=(-b-√D)/2a=(-(-5)-13)/2*4=-8/8= -1.

***

a=3;  b=-5;  c=(-a+9);

D=b²-4ac=(-5)²-4*3*(-a+9)=25+12a-108=12a-83;

12a-83<0;

12a=83;

a=83/12

a=6  11/12;

При a<6  11/12 D<0 - нет корней.

***

???