1. Үнді өзенінің жоғарғы ағысына бес өзен келіп қосылады. Бұл аймақ қалай аталады?
2. Үндістанға солтүстіктен келген көшпелі тайпаларды ата?
3. Үнді қыздарының ұлттық киімі қалай аталады?
4. Б. з. б ҮІ ғасырларда Ганга өзенінің төменгі ағысы бойында пайда болған мемлекет?
5. Үндістанның Агра қаласында орналасқан тарихи ескерткішті атаңыз?
6. Үндістанның солтүстігінен басталып, оңтүстік шығысқа қарай ағатын өзен?
7. Өз дәрежесі бойынша өмір сүруге тиісті тұйық топ?
8. Үнділерде тайпа көсемдері қалай аталған?
9. Маурия әулетінің негізін қалаған кім?
10. Брахма құдайдың аяғынан жаралған төртінші топ өкілдері?
1) проверяем условие при наименьшем возможном значении n.
n>5, значит проверяем условие при n=6
Верно!
2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:
3) Тогда при n=k+1 должно выполняться неравенство:
Вернемся к неравенству из второго пункта и домножим его на 2:
Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:
по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)
Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5
Если , а , при k>5
То есть, , при k>5, то по закону транзитивности:
, при k>5 - ч.т.д
1. Үнді өзенінің жоғарғы ағысына бес өзен келіп қосылады. Бұл аймақ қалай аталады?
2. Үндістанға солтүстіктен келген көшпелі тайпаларды ата?
3. Үнді қыздарының ұлттық киімі қалай аталады?
4. Б. з. б ҮІ ғасырларда Ганга өзенінің төменгі ағысы бойында пайда болған мемлекет?
5. Үндістанның Агра қаласында орналасқан тарихи ескерткішті атаңыз?
6. Үндістанның солтүстігінен басталып, оңтүстік шығысқа қарай ағатын өзен?
7. Өз дәрежесі бойынша өмір сүруге тиісті тұйық топ?
8. Үнділерде тайпа көсемдері қалай аталған?
9. Маурия әулетінің негізін қалаған кім?
10. Брахма құдайдың аяғынан жаралған төртінші топ өкілдері?
1) проверяем условие при наименьшем возможном значении n.
n>5, значит проверяем условие при n=6
Верно!
2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:
3) Тогда при n=k+1 должно выполняться неравенство:
Вернемся к неравенству из второго пункта и домножим его на 2:
Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:
по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)
Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5
Если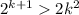 , а
, а 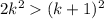 , при k>5
, при k>5
То есть,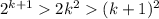 , при k>5, то по закону транзитивности:
, при k>5, то по закону транзитивности: