Выпишите коэффициент линейного уравнения с двумя переменными (а,b,c)
1)x-y+4=0
2)4y+3x-7=0

Показать ответ

Ответ:

Онелик

30.03.2020 22:04

Решение:

Рассуждать при решении задачи нужно так:

На первое место в наше число мы можем поставить любую из $\textsl {5}$ имеющихся цифр ( $\textsl {1, 2, 5, 7, 8}$ ). То есть, у нас $\textsl{5}$ и никакой из них не ограничивается законом.Со вторым местом небольшая проблема: мы не можем любую из $\textsl{5}$ цифр туда поставить, так как одна из них уже была использована. Значит, мы можем поставить на почетное второе место любую из $\textsl{4}$ оставшихся цифр.Для третьего места есть ровно $\textsl{5 - 2 = 3}$ так как

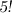
цифры из $\textsl{5}$ уже использовались).Не потеряем нить рассуждения и заметим, что для четвертого места ровно $\textsl{2}$ а для пятого, последнего, - не иначе, как одно.Итого мы будем иметь $\textsl {5 * 4 * 3 * 2 * 1 = 120}$

А можно, без всяких лирических отступлений, сказать, что чисел мы можем выставить в ряд $\textsl{5!}$

$\textsl{5! = 5 * 4 * 3 * 2 * 1 = 120}$ .

При этом формула для $\textsl{n!}$ ("эн факториал") такая: $\textsl{n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1}$ .

Задачу уже мы решили!

ответ: $\thefontsize\Large \boxed{\bold{\texrsl{120}}}$ .

0,0(0 оценок)

Ответ:

gshsjtzjts

17.05.2020 05:58

9^2+24xy+16y^2=(3x+4y)^2=(3x+4y)(3x+4y)

возможно 5 случая:

1) допустим, х-отрицательное, а y положительноетогда сумма (3x+4y) будет отрицательной, а произведение (3x+4y)(3x+4y) будет положительно.(тоже самое будет, если наоборот y-отрицательное, а x положительное)

2) допустим, х и y отрицательные,тогда сумма (3x+4y) будет положительна и произведение (3x+4y)(3x+4y) тоже будет положительно.

3) допустим, х и y положительные, тогда сумма (3x+4y) будет положительна и произведение (3x+4y)(3x+4y) соответственно будет положительно

4) допустим любая из переменных x или y=0, тогда независимо от неравной нулю переменной произведение (3x+4y)(3x+4y) будет положительно

и 5) самый простой случай, когда и х и y =0, тогда и сумма и произведение будут равны нулю, т.е. неотрицательны.

во всех 4х случаях выходит, что выражение неотрицательно, ч.т.д.

0,0(0 оценок)

Популярные вопросы: Алгебра