‼️‼️‼️‼️‼️‼️‼️‼️Выпишите количество учащихся каждого класса, обучающихся в вашей школе. По этим данным найдите: 1) объем и размах; 2) составьте интер вальную таблицу частот (относительных частот); 3) постройте гистограмму частот; 4) составьте таблицу частот (относительных частот) соответству ющего вариационного ряда; 5) постройте полигон частот вариационного ряда; 6) постройте комуляту частот; 7) моду и медиану, среднее значение вариационного ряда; 8) дисперсию и стандартное отклонение. 5а-23
6а-24
7а-22
8а-22
9а-23
10а-11
11а-7
​

По условию известно, что режимов освещения было не больше 5. То есть их могло быть:

1, 2, 3, 4, 5

Так как существует также полное отключение освещения, всего состояний может быть:

2, 3, 4, 5, 6

Найдем, сколько раз нужно нажать на кнопку, чтобы независимо от точного количества режимов вернуться в тот же самый режим. Для этого, нужно найти число, которое делится на 2, 3, 4, 5, 6 без остатка. То есть, другими словами нужно найти НОК этих чисел.

Таким образом, если нажать на кнопку 60 раз, то мы перейдем к такому же состоянию, с которого все начиналось.

По условию сейчас включен первый режим, также известно, что именно перед первым режимом идет состояние полного отключения. Значит, нажав на кнопку 60 раз мы вернемся к первом режиму, а если мы нажмем на кнопку на 1 раз меньше, то есть 59 раз, то мы полностью выключим свет.

Найденный является простейшим с той точки зрения, что нажать на кнопку можно и большее количество раз, а именно любое количество, задаваемое формулой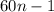 , где 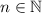, и свет также будет отключен.

ответ: нажать на кнопку 59 раз

В решении.

Объяснение:

№2 Яке найбільше натуральне значення х задовольняє нерівність 18-3(х-15)>11x

N°3. Яке найменше ціле значення а задовольняє нерівність: а² + 4a < (a + 2)²

№2 Какое наибольшее натуральное значение х удовлетворяет неравенству 18-3(х-15)>11x?

18 - 3(х-15) > 11x

18 - 3х + 45 > 11x

63 - 3x > 11x

-3x - 11x > -63

-14x > -63

14x < 63   знак меняется при делении и умножении на -1;

х < 4,5

Решение неравенства: х∈(-∞; 4,5).

Наибольшее целое значение: х = 4.

№3. Какое наименьшее целое значение а удовлетворяет неравенству: а² + 4a < (a + 2)²?

а² + 4a < (a + 2)²

а² + 4а < a² + 4a + 4

а² + 4а - a² - 4a - 4 < 0

-4 < 0

Решение неравенства: x ∈ R (х может быть любым).

Не существует наименьшего целого значения а, которое удовлетворяет данному неравенству.