С этого уравнения видно, что коэффициент возле переменной является значением производной функции в точке касания. Найдём же эту точку.
Проведём проверку найденных корней:
Первый корень дал нам уравнение другой касательной,он нам не подходит
Мы нашли абсциссу точки прикосновения, это -2
ответ: х= -2
2) Нужно найти производную функции и приравнять её к нулю, чтобы проверить критические точки на наличие экстремума
Мы нашли стационарную точку х = 3.5 , проверим её на экстремум с метода интервалов.
Подставляю в нашу производную значения с интервалов (подставляем только в числитель, так как знаменатель всегда положителен и мы это доказали выше)
Получаем такие знаки на интервалах:
Видим, что производная при переходе через точку х = 3.5 меняет свой знак с минуса на плюс, что является достаточным условием существования минимума функции в данной точке.
1) Уравнение касательной имеет вид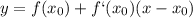
С этого уравнения видно, что коэффициент возле переменной является значением производной функции в точке касания. Найдём же эту точку.
Проведём проверку найденных корней:
Первый корень дал нам уравнение другой касательной,он нам не подходит
Мы нашли абсциссу точки прикосновения, это -2
ответ: х= -2
2) Нужно найти производную функции и приравнять её к нулю, чтобы проверить критические точки на наличие экстремума
Мы нашли стационарную точку х = 3.5 , проверим её на экстремум с метода интервалов.
Подставляю в нашу производную значения с интервалов (подставляем только в числитель, так как знаменатель всегда положителен и мы это доказали выше)
Получаем такие знаки на интервалах:
Видим, что производная при переходе через точку х = 3.5 меняет свой знак с минуса на плюс, что является достаточным условием существования минимума функции в данной точке.
ответ: х = 3.5 - точка минимума функции
ответ: (3 ;-4 ) ; (-4 ; -11).
Объяснение: Выразим в каждом из уравнений у через х:
1)х²+у=5; у= -х²+5 -квадратичная функция,
график парабола, ветви направлены вниз, т.к. а= -1 <0.
(0;5) - координаты вершины параболы,
х=0 - ось симметрии параболы.
Составим таблицу из семи точек, в центре
поставим координаты вершины:
х -4 -3 -1 0 1 3 4
у -11 -4 4 5 4 -4 -11
2) х-у=7; -у= -х+7; у=х-7 - линейная функция,
график - прямая. Составим таблицу из двух точек:
х 0 -6
у -7 -13
3) Построим на одной координатной плоскости графики
функций и найдём координаты точек пересечения:
(см.построение на фото).
А( 3; -4) и В(-4 ;-11 ) - точки пересечения графиков,
координаты которых являются графическим
решением системы уравнений.
ответ: (3 ;-4 ) ; (-4 ; -11).