выполнить контрольную работу ​

Все неравенства сравнивают с нулем.

Поэтому переносим 1 влево

и приводим к общему знаменателю:

Дробь отрицательна, когда числитель и знаменатель имеют разные знаки:

    или  

    или  

Умножаем первое неравенство каждой системы на (-1)

и меняем знак неравенства:

    или  

Выбираем пересечение множеств, заданных каждым неравенством системы:

   или    

О т в е т. (-∞; 0) U (1; +∞)

Умножаем числитель на (-1) и меняем знак

Решаем методом интервалов:

находим нули числителя:

х=1

и нули знаменателя:

х=0

Эти две точки разбивают числовую прямую на три промежутка. Находим знак дроби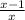  на каждом промежутке и

расставляем знаки:

__+___ (0) __-__ (1) __+__

О т в е т. (-∞; 0) U (1; +∞)

По определению:

1) область определения симметрична относительно 0;

2) для любого х из области определения f(-x)=f(x)

А)

Область определения [-3;3] - симметрична относительно 0;

f(x)=√(6-x²)

f(-x)=√(6-(-x)²)=√(6-x²)

f(-x)=f(x)

О т в е т. Является четной

Б)

Область определения (-∞;+∞) - симметрична относительно 0;

f(x)=x|x|

f(-x)=-x|-x|=-x|x|

f(-x)=- f(x)

О т в е т. НЕ является четной

B)

Область определения

x³-x≠0

x(x²-1)≠0

x≠0; x≠±1

(-∞;-1)U(-1;0)U(0;1)(1;+∞) - симметрична относительно 0;

f(x)=(x³-x²)/( (x³-x)

f(-x)=(-x³-x²)/( (-x³+x)=(x³+x²)/ (x³-x)

f(-x)≠ - f(x)

О т в е т. НЕ является четной