Выполнить тест. Если верно выполнить все задания и выписать все
соответствующие буквы, получится ключевое слово.
1.Какая точка принадлежит графику функции
у х
?
А) (0,5, 0,25);
О) (0,01; 0,1);
В) (25; -5);
Е) (0; 4);
Р) (4;16).
2. Найдите, при каких значениях а, точка (а;5) принадлежит
графику функции квадратного корня
у х .
Н) 0,25;
К) 25;
У)
5
;
И) 2,5;
Ч) 2.
3. Зная, что
f (x) х , решите уравнение f(x−2)=8.
Г) 6;
О) 16;
И)
6
;
С) 36;
Е) 66.
4. Найдите наименьшее значение функции
у х 3
на отрезке [–
2;6].
М) 3;
П) -2;
Л) 0;
А) 1;
И) -1.
5. Укажите область определения функции
у х 11.
Ы)
х 11
;
З)
х 11
;
Н)
х 11
;
У)
х 11
;
Я)
х 0 .
6. Найдите наибольшее значение функции
у х 1
на отрезке
[1;10].
О) 1;
Ж) 4;
Х) 2;
А) 3;
Д) 4.
7. Даны точки: M(81; 9), N(36; –6), P(–9; –3), Q(121; 11), T(4; –2),
F(5; -2,5). Укажите те из них, которые принадлежат графику
функции
у х .
A) M, Q, T;
Прикрепить
в
Kundelik.kz
Е) N, T;
И) M, N, P, Q, T, F;
Р) M, Q;
Ф) P, T, F.
8.Какое из ниже приведенных высказываний является истинным
относительно уравнения
2 2
2
х х
?
Л) уравнение имеет один корень, причем он положительный;
К) уравнение имеет один корень, причем он отрицательный;
У) уравнение имеет два корня, причем они различны по знаку;
Й) уравнение имеет два корня, причем они одинаковы по знаку;
И) уравнение не имеет корней.
9. Из точек M(81; 9), N(36; -6), P(-9; -3), Q(121; 11), T(4; -2),
F(5; -2,5), выберите те, которые будут принадлежать графику
функции
у х .
У) N, T;
Ц) N, T, F;
А) M, N, P, Q, T;
Ш) M, Q;
И) N, P, T, F.
10. Укажите целое число, расположенное между числами
4 5
и
82 .
У) 7;
С) 8;
М) 9;
И) 10;
Н) 11.
В ответ запишите ключевое слово
(???) за 60 мин
Объяснение:
1) 1/55 кувшина за 1 мин выпивают Двалин и Бомбур
2) 1/110 кувшина за 1 мин выпивают Бомбур и Глоин
3) 1/165 кувшина за 1 мин выпивают Глоин и Двалин
4)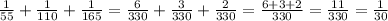
- удвоенное кол-во кувшина за 1 мин выпивают Двалин и Бомбур и Глоин
5)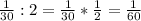
- кол-во кувшина за 1 мин выпивают Двалин и Бомбур и Глоин
6)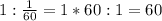
- за столько минут выпьют этот кувшин трое гномов
----------------------
ПЛОХАЯ ЗАДАЧА с кривыми данными - получается Двалин и Бомбур выпьют кувшин быстрее чем они выпьют кувшин втроем
---------------------------
=>Двалин и Бомбур выпивают 6 кувшинов компота за 330 мин, Бомбур и Глоин выпивают 3 кувшина за 330 мин, Глоин и Двалин — 2 кувшина за 330 мин.
=> 6>2+3 (если не брать в учет Глоина, для оценки)
(???) за 60 мин
Объяснение:
1) 1/55 кувшина за 1 мин выпивают Двалин и Бомбур
2) 1/110 кувшина за 1 мин выпивают Бомбур и Глоин
3) 1/165 кувшина за 1 мин выпивают Глоин и Двалин
4)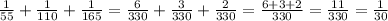
- удвоенное кол-во кувшина за 1 мин выпивают Двалин и Бомбур и Глоин
5)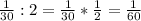
- кол-во кувшина за 1 мин выпивают Двалин и Бомбур и Глоин
6)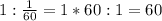
- за столько минут выпьют этот кувшин трое гномов
----------------------
ПЛОХАЯ ЗАДАЧА с кривыми данными - получается Двалин и Бомбур выпьют кувшин быстрее чем они выпьют кувшин втроем
---------------------------
=>Двалин и Бомбур выпивают 6 кувшинов компота за 330 мин, Бомбур и Глоин выпивают 3 кувшина за 330 мин, Глоин и Двалин — 2 кувшина за 330 мин.
=> 6>2+3 (если не брать в учет Глоина, для оценки)