Выполнить умножения
а) 2х(х2 + 8x – 3),
б) -За(а2 + 2ав – 5в),
В) 4х3(ax2 + а3х – 2а2).
Упростить выражение:
а) -2х(х + 4) +5(х2 – 3х),
б) 2а(За – а2) – 4a(2а2 – 5а),
В) x(2x – 1) -3x( 3 – х).
Решить уравнение:
а) 5x(x-4) -x(3 + 5x) =4,
б) 7x – 2х2 + 4 = x(5 – 2х),
B) 2x(3х – 2) -3(х2 – 4x) == 3х(х – 7) +2.

Показать ответ

Ответ:

dron2003

20.12.2020 01:33

ответ: 6 л .

Пусть 8 литров водного раствора кислоты содержит х литров салициловой кислоты.

Тогда в этом растворе кислоты будет х/8 частей.

Добавили ещё 16 л раствора, в которых содержится 60% кислоты, то есть кислоты там будет 16*0,6=9,6 л .

Теперь есть (8+16)=24 л раствора, в котором содержится (х+9,6) л кислоты . Значит кислоты содержится (х+9,6)/24 частей .

Но в результате кислоты стало на 10% меньше , чем было, то есть стало (х/8-0,1) частей кислоты . Составим уравнение .

$\dfrac{x+9,6}{24}=\dfrac{x}{8}-0,1 \ \ \Big|\cdot 24\\\\x+9,6=3x-2,4\ \ \ ,\ \ \ 9,6+2,4=3x-x\ \ ,\ \ \ 2x=12\ \ ,\ \ x=6$

Изначальный объём кислоты в восьмилитровом растворе был равен

6 литрам .

Проверим вычисления.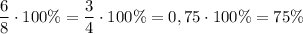 $\dfrac{6}{8}\cdot 100\%=\dfrac{3}{4}\cdot 100\%=0,75\cdot 100\%=75\%$

$\dfrac{6+9,6}{24}\cdot 100\%=\dfrac{15,6}{24}\cdot 100\%=\dfrac{156}{240}\cdot 100\%=0,65\cdot 100\%=65\%\\\\75\%-65\%=10\%$

0,0(0 оценок)

Ответ:

Инна1234432114865

06.12.2021 20:45

5 (км/час) - скорость до встречи.

Объяснение:

Фродо с друзьями под предводительством Гэндальфа вышли из Шира. Путешествие в трактир «Гарцующий пони», в котором заночевали хоббиты и маг, проходило с разной средней скоростью — пока компания не наткнулась на назгула, дело шло быстрее, а после этой встречи бодрый дух друзей поугас, и они пошли медленнее на 4 км/ч. В целом расстояние до трактира составляло 12 км, которое было преодолено за 4 часа, причём первая и вторая части пути заняли одно и то же время. С какой скоростью происходило движение до встречи с назгулом?

Формула движения: S=v*t

S - расстояние v - скорость t – время

х - скорость до встречи.

х-4 - скорость после встречи.

2 часа - время до встречи (по условию).

2 часа - время после встречи (по условию).

Расстояние общее известно, уравнение:

х * 2 + (х-4) * 2 = 12

2х+2х-8=12

4х=20

х=5 (км/час) - скорость до встречи.

5-4=1 (км/час) - скорость после встречи.