Выполнить задания:
1. Функция задана формулой у = -4х - 2. Найдите значение аргумента, при котором функция принимает значение, равное 14
2. Функция задана формулой у = 15х - 3. Найдите значение функции, соответствующее значению аргумента, равному 1/5.
3. Постройте график функции, заданной формулой у = -4х + 8. С графика найдите координаты точек пересечения графика с осями координат.
4. Функция задана формулой у = 0,7х - 3,5. Найдите координаты точки пересечения графика этой функции с осью абсцисс
5. Функция задана формулой у = -2х - 7. Найдите координаты точки пересечения графика этой функции с осью ординат
6. Какая из точек А(3:-3) и В(1;5) принадлежит графику функции у = -4х + 9
7. Найдите координаты точки пересечения графиков функций у = 3х - 11 и у = 5 - х
8. Найдите координаты точки пересечения графиков функций у =-3х +1 и
у = -4х+5.
9. Функция задана формулой у = -6х + b. График этой функции проходит через точку А(2;-9). Найдите b
10. При каком значении k график функции у = kx + 2 проходит через точку В (3;8):

Показать ответ

Ответ:

AlexBennet

01.05.2020 12:18

Пусть двузначное число составлено из двух цифр a и b, причём a≠0 и b≠0. Тогда число можно представить в виде суммы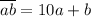 $\overline{ab}=10a+b$ .

Сразу проверим случай a=b :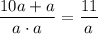 $\dfrac {10a+a}{a\cdot a}=\dfrac {11}{a}$ . Так как число 11 - простое (делители 1 и 11), только число 11 будет кратно 1·1. Другие двузначные числа не подходят под условие.

Число кратно произведению цифр ab.

$\dfrac {10a+b}{ab}=k,~k\in N\\\\kab=10a+b~~|:b\neq 0 \\\\ka=\dfrac{2\cdot 5\cdot a}b+1$

Так как числа ka и 1 - целые, значит, дробь должна тоже стать целым числом. Знаменатель b должен быть равен 1 или сократиться.

$1)~\boldsymbol{b=1;}~~a=\dfrac {b}{kb-10}=\dfrac 1{k-10};~~~k=11; \boldsymbol{a=1}$

$2)~\boldsymbol{b=2;}~~\dfrac {10a+2}{2a}=5+\dfrac 1{a};~~~\boldsymbol{a=1}$

$3)~\boldsymbol{b=5;}~~\dfrac {10a+5}{5a}=2+\dfrac 1{a};~~~\boldsymbol{a=1}$

4) Число a или число 2a должны быть кратны цифре b. Возможные пары, помимо рассмотренных : (2;4), (3,6), (4,8), (6,3), (8,4), (9,3)

a = 2; b = 4;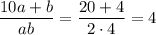 $\dfrac {10a+b}{ab}=\dfrac {20+4}{2\cdot4}=4$

a = 3; b = 6;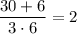 $\dfrac {30+6}{3\cdot6}=2$

Остальные варианты не подходят

a = 4; b = 8;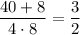 $\dfrac {40+8}{4\cdot8}=\dfrac32$ a = 6; b = 3;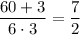 $\dfrac {60+3}{6\cdot3}=\dfrac{7}2$

a = 8; b = 4;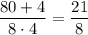 $\dfrac {80+4}{8\cdot4}=\dfrac{21}8$ a = 9; b = 3;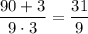 $\dfrac {90+3}{9\cdot3}=\dfrac{31}9$

ответ : 11, 12, 15, 24, 36

0,0(0 оценок)

Ответ:

малинка188

01.05.2020 12:18

Чтобы не искать число за числом по калькулятору, будем рассуждать логически:

Попробуем составить уравнение, которое нам.

Нам нужно, чтобы двузначное число делилось на произведение своих цифр. Представим само число как сумму десятков и единиц:

10x + y

А произведение представим просто:

x × y

Теперь уравняем их:

10x + y = x × y

x ≠ 0

y ≠ 0

1. Возьмём x = 1

10 × 1 + y = 1 × y

10 + y = y

Теперь разделим левую часть на правую. Суть этого уравнения состоит в том, что левая часть уравнения должна делиться на правую без остатка. Таким образом мы и найдём все двузначные числа, которые кратны произведению своих цифр.)

Значится:

(10 + y) ÷ y = 10/y + y/y = 10/y + 1

Смотрим. В сумме должно получится ЦЕЛОЕ число. Чтобы оно получилось, надо знать, на что делится десятка без остатка. А делится она на 1, 2 и 5.) Значит, "игрек" будет равен этим числам. первые три числа уже нашли. Это:

11, 12 и 15.

2. Теперь возьмём x = 2

10 × 2 + y = 2 × y

20 + y = 2y

(20 + y) ÷ 2y = 20/2y + y/2y = 10/y + 1/2

Опять же - в сумме должно получится ЦЕЛОЕ число. Значит надо думать, на что поделить десятку, чтобы потом полученное число сложить с дробью 1/2 (0,5) и в конечном счёте получить целое число.

Очевидно, что это цифра "4", т.к. 10 ÷ 4 = 2,5. А 2,5 + 0,5 = 3 - целое число.)

Значит, y = 4. В итоге получаем ещё одно число, кратное произведению своих цифр:

24.

3. Теперь x = 3

10 × 3 + y = 3 × y

30 + y = 3y

(30 + y) ÷ 3y = 30/3y + y/3y = 10/y + 1/3

Те же манипуляции. Ищем, на что дожна делиться десятка, чтобы полученное число прибавить к 1/3 и получить целое число.)

Это цифра "6". y = 6

10/6 = 5/3 = 1 целая и 2/3. 1 целая и 2/3 + 1/3 = 3.

Нашли ещё одно число:

36.