Алгебра: Выполните дейстия (3/2x-1 ÷ 3x-1/4x^2-1 - 6/3x-1)*3/2x-1 +( 3x-1/3x-10)-1

Первый Решение ищем как сумму общего решения однородного уравнения, соответствующего данному неоднородному, и частного решения данного неоднородного уравнения.Составим однородное уравнение, соответствующее данному неоднородному:Решаем уравнение с разделяющимися переменными:Общее решение однородного уравнения:Частное решение ищем в виде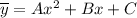 .Найдем производную:Подставим в уравнение:Условие равенства левой и правой частей:Частное решение неоднородного уравнения:Искомое решение:Второй Решение ищем в виде...

Выполните дейстия (3/2x-1 ÷ 3x-1/4x^2-1 - 6/3x-1)*3/2x-1 +( 3x-1/3x-10)-1

Показать ответ

Ответ:

kostija73

26.11.2020 02:41

в система уравнений состоит из двух простых уравнений, но как то не похожей на обычные уравнения, так ведь?!

давай обьясню на примере:

y=2+5x

9x+3y=10

например вот этот. тут первый надо поставить во второй, и в то место, где та же буква, которая за равно стоит, то есть:

9x+3*(2+5x)=10 мы получили одно уравнение, с одной буквой. решается оно как обычное. но отличается еще одним свойством, в конце, когда найдем "х" нужно будет найти еще и "у".

у у нас равен 2+5х, если ты найшла х, то с лехкостью сможешь его подставить его вместо буквы, и получишь простое выражение. допустим у тебя х равен 3, то получится след:

у=2+5*3=2+15=17

но к большому несчастью еще есть один вариант системы, расмотрим на примере:

5х+6у=58

2у-9х=12

хм, что же делать в этом случае?!

самое главное, не бояться его и не пониковать. присмотрись к нему...

как думаешь, из выражения 2у-9х=12 можно вынести хотя бы одну букву?!

давай попробуем: 2у=12+9х

у=(12+9х)/2

а теперь, как и в первом случае, подставляем в другое уравнение это и получаем:

5х+6((12+9х)/2)=58

и решаешь

и в конце так же находишь у

вот и все, удачи)

0,0(0 оценок)

Ответ:

ilinasmirnova5

06.10.2020 05:01

y'=y-x^2

y'-y=-x^2

Первый

Решение ищем как сумму общего решения однородного уравнения, соответствующего данному неоднородному, и частного решения данного неоднородного уравнения.

Составим однородное уравнение, соответствующее данному неоднородному:

y'-y=0

Решаем уравнение с разделяющимися переменными:

y'=y

$\dfrac{dy}{dx} =y$

$\dfrac{dy}{y} =dx$

$\int\dfrac{dy}{y} =\int dx$

$\ln|y| =x+C$

Общее решение однородного уравнения:

$y=e^{x+C}$

Частное решение ищем в виде $\overline{y}=Ax^2+Bx+C$ .

Найдем производную:

$\overline{y}'=2Ax+B$

Подставим в уравнение:

2Ax+B-Ax^2-Bx-C=-x^2

-Ax^2+(2A-B)x+(B-C)=-x^2

Условие равенства левой и правой частей:

$\begin{cases} -A=-1\\ 2A-B=0 \\ B-C=0 \end{cases}$

$\begin{cases} A=1\\ 2-B=0 \\ C=B \end{cases}$

$\begin{cases} A=1\\ B=2 \\ C=2 \end{cases}$

Частное решение неоднородного уравнения:

$\overline{y}=x^2+2x+2$

Искомое решение:

$\boxed{y=e^{x+C}+x^2+2x+2}$

Второй

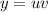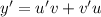Решение ищем в виде произведения двух ненулевых функций y=uv . Тогда y'=u'v+v'u .

u'v+v'u-uv=-x^2

Пусть сумма первого и третьего слагаемого в левой части равна нулю:

u'v-uv=0

u'-u=0

$\dfrac{du}{dx} -u=0$

$\dfrac{du}{dx}=u$

$\dfrac{du}{u}=dx$

$\ln|u|=x$

u=e^x

Тогда второе слагаемое в левой части равно правой части:

v'u=-x^2

$v'\cdot e^x=-x^2$

$\dfrac{dv}{dx} \cdot e^x=-x^2$

$dv=-x^2e^{-x}dx$

$\int dv=-\int x^2e^{-x}dx$

Интеграл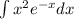 $\int x^2e^{-x}dx$ вычислим отдельно. Будем использовать интегрирование по частям: 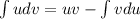$\int udv=uv-\int vdu$ (не записывая произвольную константу):

$\int x^2e^{-x}dx=\left=-x^2e^{-x}-\int(-e^{-x}\cdot2xdx)=\\=-x^2e^{-x}+2\int xe^{-x}dx=\left=\\=-x^2e^{-x}+2\left(x\cdot(-e^{-x})-\int(-e^{-x}dx)\right)=-x^2e^{-x}+2\left(-xe^{-x}+\int e^{-x}dx\right)=\\=-x^2e^{-x}+2\left(-xe^{-x}-e^{-x}\right)=-x^2e^{-x}-2xe^{-x}-2e^{-x}=-(x^2+2x+2)e^{-x}$