№1 а
№2 а) (9/2; 10)
б) (54/37; 34/37)
Объяснение:
№1
а)
3(5+3y) +2y = 4
15+9y+2y=4
15+11y=4
11y=-11
y= -1
x= 5+3*(-1) = 2
ответ: (2; -1)
б)
2x-3(6-3x) = 7
2x-18+9x = 7
-18+11x = 7
11x = 25
x = 25/11
y = 6-3* (25/11) = -(9/11)
ответ: (25/11 ; - 9/11)
Нам подходит только система под буквой А
( ты можешь просто подставить (2; -1) в системы и сразу получить результат, но я не знаю, разрешают вам так делать или нет, поэтому расписала системы )
№2
4* 9/2 -y = 8
2*9-y = 8
18-y = 8
y = 10
ответ: (9/2; 10)
3x+17(-2+2x) = 20
3x-34+34x = 20
37x-34 = 20
37x = 54
x = 54/37
y = -2+2* (54/37) = -2 + 108/37 = 34/37
ответ: (54/37; 34/37)
у' = ( х³ - 2х² + х - 2 )' = ( х³ )' - ( 2х² )' + ( х )' - ( 2 )' = 3х² - 4х + 1
у' = 0 ⇒ 3х² - 4х + 1 = 0
D = (-4)² - 4•3•1 = 16 - 12 = 4 = 2²
x₁ = ( 4 - 2 )/6 = 2/6 = 1/3
x₂ = ( 4 + 2 )/6 = 6/6 = 1
y' [ 1/3 ][ 1 ]> x
y __↑__[ x (max) ]__↓__[ x (min) ]__↑__> x
Значит, точка минимума ⇒ х = 1
ОТВЕТ: 1
2) Найдите точку максимума функции у = 9 - 4х + 4х² - х³
у' = - 4 + 8х - 3х² ; у' = 0
- 4 + 8x - 3х² = 0
3x² - 8x + 4 = 0
D = (-8)² - 4•3•4 = 64 - 48 = 16 = 4²
x₁ = ( 8 - 4 )/6 = 4/6 = 2/3
x₂ = ( 8 + 4 )/6 = 12/6 = 2
y' [ 2/3 ][ 2 ]> x
y __↓__[ x (min) ]__↑__[ x (max) ]__↓__> x
Значит, точка максимума ⇒ х = 2
ОТВЕТ: 2
3) Найдите точку минимума функции у = х³ - 3,5х² + 2х - 3
у' = 3х² - 7х + 2 ; у' = 0 ⇒
3х²- 7х + 2 = 0
D = (-7)² - 4•3•2 = 49 - 24 = 25 = 5²
x₁ = ( 7 - 5 )/6 = 2/6 = 1/3
x₂ = ( 7 + 5 )/6 = 12/6 = 2
y' [ 1/3 ][ 2 ]> x
Значит, точка минимума ⇒ х = 2
4) Найдите точку максимума функции у = х³ + х² - 8х - 7
у' = 3х² + 2х - 8 ; у' = 0 ⇒
3х² + 2х - 8 = 0
D = 2² - 4•3•(-8) = 4 + 96 = 100 = 10²
x₁ = ( - 2 - 10 )/6 = - 12/6 = - 2
x₂ = ( - 2 + 10 )/6 = 8/6 = 4/3
y' [ - 2 ][ 4/3 ]> x
y ___↑___[ x (max) ]__↓__[ x (min) ]__↑__> x
Значит, точка максимума ⇒ х = - 2
ОТВЕТ: - 2
5) Найдите точку минимума функции у = х³ - 4х² - 3х - 12
у' = 3х² - 8х - 3 ; у' = 0 ⇒
3х² - 8х - 3 = 0
D = (-8)²- 4•3•(-3) = 64 + 36 = 100 = 10²
x₁ = ( 8 - 10 )/6 = - 2/6 = - 1/3
x₂ = ( 8 + 10 )/6 = 18/6 = 3
y' [ - 1/3 ][ 3 ]> x
y ___↑__[ x (max) ]__↓__[ x (min) ]__↑__> x
Значит, точка минимума ⇒ х = 3
ОТВЕТ: 3
6) Найдите точку максимума функции у = х³ + 8х² + 16х + 3
у' = 3х² + 16х + 16 ; у' = 0 ⇒
3х² + 16х + 16 = 0
D = 16² - 4•3•16 = 16•( 16 - 12 ) = 16•4 = 4²•2² = 8²
x₁ = ( - 16 - 8 )/6 = - 24/6 = - 4
x₂ = ( - 16 + 8 )/6 = - 8/6 = - 4/3
y' [ - 4 ][ - 4/3 ]> x
y __↑__[ x (max) ]__↓__[ x (min) ]__↑___> x
Значит, точка максимума ⇒ х = - 4
ОТВЕТ: - 4
7) Найдите точку минимума функции у = х³ + х² - 16х + 5
у' = 3х² + 2х - 16 ; у' = 0 ⇒
3х² + 2х - 16 = 0
D = 2² - 4•3•(-16) = 4•( 1 + 48 ) = 4•49 = 2²•7² = 14²
x₁ = ( - 2 - 14 )/6 = - 16/6 = - 8/3
x₂ = ( - 2 + 14 )/6 = 12/6 = 2
y' [ - 8/3 ][ 2 ]> x
8) Найдите точку максимума функции у = х³ + 4х² + 4х + 4
у' = 3х² + 8х + 4 ; у' = 0 ⇒
3х² + 8х + 4 = 0
D = 8² - 4•3•4 = 64 - 48 = 16 = 4²
x₁ = ( - 8 - 4 )/6 = - 12/6 = - 2
x₂ = ( - 8 + 4 )/6 = - 4/6 = - 2/3
y' [ - 2 ][ - 2/3 ]> x
9) Найдите точку минимума функции у = х³ - 4х² - 8х + 8
у' = 3х² - 8х - 8 ; у' = 0 ⇒
3х² - 8х - 8 = 0
D = (-8)² - 4•3•(-8) = 64 + 96 = 160 = (4√10)²
x₁ = ( 8 - 4√10 )/6 = (4 - 2√10)/3
x₂ = ( 8 + 4√10 )/6 = (4 + 2√10)/3
y' [ (4-2√10)/3 ][ (4+2√10)/3 ]> x
y ___↑__[ x (max) ]↓[ x (min) ]↑___> x
Значит, точка минимума ⇒ х = (4+2√10)/3
ОТВЕТ: (4+2√10)/3
10) Найдите точку максимума функции у = х³ + 5х² + 3х + 2
у' = 3х² + 10х + 3 ; у' = 0 ⇒
3х² + 10х + 3 = 0
D = 10² - 4•3•3 = 100 - 36 = 64 = 8²
x₁ = ( - 10 - 8 )/6 = - 18/6 = - 3
x₂ = ( - 10 + 8 )/6 = - 2/6 = - 1/3
y' [ - 3 ][ - 1/3 ]> x
y __↑__[ x (max) ]__↓__[ x (min) ]__↓__> x
Значит, точка максимума ⇒ х = - 3
ОТВЕТ: - 3
Подробнее - на -
№1 а
№2 а) (9/2; 10)
б) (54/37; 34/37)
Объяснение:
№1
а)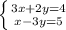
3(5+3y) +2y = 4
15+9y+2y=4
15+11y=4
11y=-11
y= -1
x= 5+3*(-1) = 2
ответ: (2; -1)
б)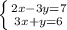
2x-3(6-3x) = 7
2x-18+9x = 7
-18+11x = 7
11x = 25
x = 25/11
y = 6-3* (25/11) = -(9/11)
ответ: (25/11 ; - 9/11)
Нам подходит только система под буквой А
( ты можешь просто подставить (2; -1) в системы и сразу получить результат, но я не знаю, разрешают вам так делать или нет, поэтому расписала системы )
№2
а)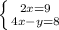
4* 9/2 -y = 8
2*9-y = 8
18-y = 8
y = 10
ответ: (9/2; 10)
б)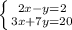
3x+17(-2+2x) = 20
3x-34+34x = 20
37x-34 = 20
37x = 54
x = 54/37
y = -2+2* (54/37) = -2 + 108/37 = 34/37
ответ: (54/37; 34/37)
у' = ( х³ - 2х² + х - 2 )' = ( х³ )' - ( 2х² )' + ( х )' - ( 2 )' = 3х² - 4х + 1
у' = 0 ⇒ 3х² - 4х + 1 = 0
D = (-4)² - 4•3•1 = 16 - 12 = 4 = 2²
x₁ = ( 4 - 2 )/6 = 2/6 = 1/3
x₂ = ( 4 + 2 )/6 = 6/6 = 1
y' [ 1/3 ][ 1 ]> x
y __↑__[ x (max) ]__↓__[ x (min) ]__↑__> x
Значит, точка минимума ⇒ х = 1
ОТВЕТ: 1
2) Найдите точку максимума функции у = 9 - 4х + 4х² - х³
у' = - 4 + 8х - 3х² ; у' = 0
- 4 + 8x - 3х² = 0
3x² - 8x + 4 = 0
D = (-8)² - 4•3•4 = 64 - 48 = 16 = 4²
x₁ = ( 8 - 4 )/6 = 4/6 = 2/3
x₂ = ( 8 + 4 )/6 = 12/6 = 2
y' [ 2/3 ][ 2 ]> x
y __↓__[ x (min) ]__↑__[ x (max) ]__↓__> x
Значит, точка максимума ⇒ х = 2
ОТВЕТ: 2
3) Найдите точку минимума функции у = х³ - 3,5х² + 2х - 3
у' = 3х² - 7х + 2 ; у' = 0 ⇒
3х²- 7х + 2 = 0
D = (-7)² - 4•3•2 = 49 - 24 = 25 = 5²
x₁ = ( 7 - 5 )/6 = 2/6 = 1/3
x₂ = ( 7 + 5 )/6 = 12/6 = 2
y' [ 1/3 ][ 2 ]> x
y __↑__[ x (max) ]__↓__[ x (min) ]__↑__> x
Значит, точка минимума ⇒ х = 2
ОТВЕТ: 2
4) Найдите точку максимума функции у = х³ + х² - 8х - 7
у' = 3х² + 2х - 8 ; у' = 0 ⇒
3х² + 2х - 8 = 0
D = 2² - 4•3•(-8) = 4 + 96 = 100 = 10²
x₁ = ( - 2 - 10 )/6 = - 12/6 = - 2
x₂ = ( - 2 + 10 )/6 = 8/6 = 4/3
y' [ - 2 ][ 4/3 ]> x
y ___↑___[ x (max) ]__↓__[ x (min) ]__↑__> x
Значит, точка максимума ⇒ х = - 2
ОТВЕТ: - 2
5) Найдите точку минимума функции у = х³ - 4х² - 3х - 12
у' = 3х² - 8х - 3 ; у' = 0 ⇒
3х² - 8х - 3 = 0
D = (-8)²- 4•3•(-3) = 64 + 36 = 100 = 10²
x₁ = ( 8 - 10 )/6 = - 2/6 = - 1/3
x₂ = ( 8 + 10 )/6 = 18/6 = 3
y' [ - 1/3 ][ 3 ]> x
y ___↑__[ x (max) ]__↓__[ x (min) ]__↑__> x
Значит, точка минимума ⇒ х = 3
ОТВЕТ: 3
6) Найдите точку максимума функции у = х³ + 8х² + 16х + 3
у' = 3х² + 16х + 16 ; у' = 0 ⇒
3х² + 16х + 16 = 0
D = 16² - 4•3•16 = 16•( 16 - 12 ) = 16•4 = 4²•2² = 8²
x₁ = ( - 16 - 8 )/6 = - 24/6 = - 4
x₂ = ( - 16 + 8 )/6 = - 8/6 = - 4/3
y' [ - 4 ][ - 4/3 ]> x
y __↑__[ x (max) ]__↓__[ x (min) ]__↑___> x
Значит, точка максимума ⇒ х = - 4
ОТВЕТ: - 4
7) Найдите точку минимума функции у = х³ + х² - 16х + 5
у' = 3х² + 2х - 16 ; у' = 0 ⇒
3х² + 2х - 16 = 0
D = 2² - 4•3•(-16) = 4•( 1 + 48 ) = 4•49 = 2²•7² = 14²
x₁ = ( - 2 - 14 )/6 = - 16/6 = - 8/3
x₂ = ( - 2 + 14 )/6 = 12/6 = 2
y' [ - 8/3 ][ 2 ]> x
y __↑__[ x (max) ]__↓__[ x (min) ]__↑___> x
Значит, точка минимума ⇒ х = 2
ОТВЕТ: 2
8) Найдите точку максимума функции у = х³ + 4х² + 4х + 4
у' = 3х² + 8х + 4 ; у' = 0 ⇒
3х² + 8х + 4 = 0
D = 8² - 4•3•4 = 64 - 48 = 16 = 4²
x₁ = ( - 8 - 4 )/6 = - 12/6 = - 2
x₂ = ( - 8 + 4 )/6 = - 4/6 = - 2/3
y' [ - 2 ][ - 2/3 ]> x
y __↑__[ x (max) ]__↓__[ x (min) ]__↑___> x
Значит, точка максимума ⇒ х = - 2
ОТВЕТ: - 2
9) Найдите точку минимума функции у = х³ - 4х² - 8х + 8
у' = 3х² - 8х - 8 ; у' = 0 ⇒
3х² - 8х - 8 = 0
D = (-8)² - 4•3•(-8) = 64 + 96 = 160 = (4√10)²
x₁ = ( 8 - 4√10 )/6 = (4 - 2√10)/3
x₂ = ( 8 + 4√10 )/6 = (4 + 2√10)/3
y' [ (4-2√10)/3 ][ (4+2√10)/3 ]> x
y ___↑__[ x (max) ]↓[ x (min) ]↑___> x
Значит, точка минимума ⇒ х = (4+2√10)/3
ОТВЕТ: (4+2√10)/3
10) Найдите точку максимума функции у = х³ + 5х² + 3х + 2
у' = 3х² + 10х + 3 ; у' = 0 ⇒
3х² + 10х + 3 = 0
D = 10² - 4•3•3 = 100 - 36 = 64 = 8²
x₁ = ( - 10 - 8 )/6 = - 18/6 = - 3
x₂ = ( - 10 + 8 )/6 = - 2/6 = - 1/3
y' [ - 3 ][ - 1/3 ]> x
y __↑__[ x (max) ]__↓__[ x (min) ]__↓__> x
Значит, точка максимума ⇒ х = - 3
ОТВЕТ: - 3
Подробнее - на -
Объяснение: