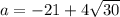Это в 3 степени График думаю построишь сам(а) по точкам, они (точки) и сам график в учебнике есть, а точку найду: х=2 у=8.
Для построения графика черти координатную плоскость, обязательно бери отрезок в 2 клетки, положительное направление укажи, подпиши оси и начало координат.
Точки могу указать, по которым график строить нужно:
х= у=
0 0
1 1
2 8
-1 -1
-2 -8
0,5 0,1
-0,5 -0,1
1,5 3,4
-1,5 -3,4
это во 2 степени Например, при х = 3 значение функции y = 3 2 = 9 , а при х = –2 значение функции y = (–2) 2 = 4 .
Изобразим график функции y = x 2 . Для этого присвоим аргументу х несколько значений, вычислим соответствующие значения функции и внесем их в таблицу.
Если: x = –3 , x = –2 , x = –1 , x = 0 , x = 1 , x = 2 , x = 3,
то: y = 9 , y = 4 , y = 1 , y = 0 , y = 1 , y = 4 , y = 9.
График думаю построишь сам(а) по точкам, они (точки) и сам график в учебнике есть, а точку найду: х=2 у=8.
Для построения графика черти координатную плоскость, обязательно бери отрезок в 2 клетки, положительное направление укажи, подпиши оси и начало координат.
Точки могу указать, по которым график строить нужно:
х= у=
0 0
1 1
2 8
-1 -1
-2 -8
0,5 0,1
-0,5 -0,1
1,5 3,4
-1,5 -3,4
это во 2 степени
Например, при х = 3 значение функции y = 3 2 = 9 ,
а при х = –2 значение функции y = (–2) 2 = 4 .
Изобразим график функции y = x 2 . Для этого присвоим
аргументу х несколько значений, вычислим соответствующие значения
функции и внесем их в таблицу.
Если:
x = –3 ,
x = –2 ,
x = –1 ,
x = 0 ,
x = 1 ,
x = 2 ,
x = 3,
то:
y = 9 ,
y = 4 ,
y = 1 ,
y = 0 ,
y = 1 ,
y = 4 ,
y = 9.
Условие. Y²+xy-4x-9y+20=0 ; y=ax+1 ; x>2
найти все значения а, при которых графики имеют одну общую точку(в нашем случае (ax+1)² + x(ax+1) -4x - 9(ax+1)+20=0 имеет единственное решение).
Подставим у = (ax+1)² в уравнение у²+xy-4x-9y+20=0, получим
Найдем дискриминант квадратного уравнения относительно x
Получим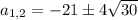
Если подставить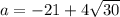
, т.е. имеется квадратное уравнение 
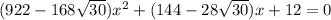, у которого корень
Если подставить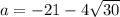
, т.е. имеется квадратное уравнение 
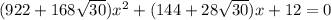, у которого корень
ответ: