Выполните вычисления, записывая каждое действие столбиком. 1 × (80 001 – 7 955) : 2 ​​84 м 67 см × 7​
34 509 × 8 + 56 789​​​ 7 кг 280 г : 4
решить

√4.5 * √72 = √4.5 *√ 9*8 = √4.5 * 3 * √8 = √4.5 * 3 * √4*2 = √4.5 * 3 * 2 * √2 = √4.5 * 6 * √2 = √4.5*√2 * 6 = √9 * 6 = 3*6 = 18
т.к выглядит по татарски , напишу письменно
корень их 4,5 умножим на корень из 72 , разложим 72 на множители- 9 и 8( что бы корень исчез)  , корень из 9 - это 3 , следовательно получаем:
корень из √4.5 * 3 * √8 . 8 тоже можно разложить на множители - это 4*2
а корень из 4 - это 2,
получаем корень из 4,5, умноженное на 3, умноженное на на 2  и ещё раз умноженное на корень из двух
3 и 2 перемножаем , получаем 6.
и теперь у нас остаётся корень из 4,5 и корень из двух
их мы тоже перемножим , получим корень из 9
а корень из 9 - это 3
получается что 6*3=18
ОТВЕТ : 18
спрашивай, если что не понятно 

Для решения запишем формулу бинома Ньютона:

Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение .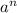

Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение .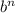

Рассмотрим многочлен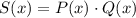 , где:

Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.

Для многочлена :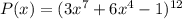

- степень определяется выражением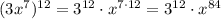 , то есть степень равна 84

- свободный член равен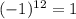

Для многочлена :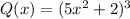

- степень определяется выражением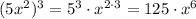 , то есть степень равна 6

- свободный член равен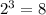

Наконец, для многочлена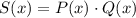 получим:

- степень определяется выражением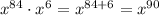 , то есть степень равна 90

- свободный член равен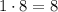

Сумма степени и свободного члена многочлена :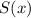

ответ: 98