Поскольку левая часть делится на 4, то и правая часть делится на 4.
Число 14- четное, но тогда и число четное
То есть среди чисел - хотя бы одно четное. Пусть произвольно, в силу симметрии задачи:
Левая часть остается четной, а значит и правая часть должна быть четной, но поскольку 7- нечетное число, то - тоже нечетное число, а значит все числа - нечетные.
Предположим, что
Поделим обе части равенства на
Предположим, что одновременно верно, что :`
Но тогда, в силу того, что все числа целые, а так-же того, что какой бы знак не имели числа x,b,c, всегда хотя бы одно из выражений :
4/c; 2/x ; 4/b ; -7/cbx - отрицательно.
Действительно, если окажется, что -7/сbx > 0 , то хотя бы одно из чисел с,b,x меньше нуля.
Поскольку, число 7/8 - cамое маленькое среди данных 4-x чисел.
То есть мы пришли к противоречию, а значит, хотя бы одно из чисел, a,b,x равно +-1. Тогда в силу симметрии задачи, в уравнении
одно из чисел a,b,c равно либо +-1 либо +-2.
1)
В силу симметрии задачи, все перестановки чисел 1,2,3 и 1,5,6 являются решениями системы.
2)
В других случаях из симметрии так же нет решений.
3)
В других случаях так же нет решений.
4)
Таким образом больше решений нет.
Осталось рассмотреть:
Решений нет.
Примечание: можно было получить разложение сразу для произвольного a, а потом просто подставлять в него различные a. Так было бы немного быстрее и компактнее.
Получено по тому же самому алгоритму, что и в данных примерах.
То есть подставляем : a=+-1 ; +-2; 0 получаем все те же самые случаи.
2cos(3π/20) * cos(π/10)
Объяснение:
Для таких примеров есть формула:
cos(a) + cos(b) = 2cos((a+b)/2) * cos((a-b)/2)
Подставим в неё наши значения
cos(π/4) + cos(π/20) = 2cos((π/4 + π/20)/2) * cos((π/4 - π/20)/2)
И вычисляем, при этом приводя к общему знаменателю и т.д., получим(вычисления, углы суммируем, вычитаем и делим на два):
2cos(3π/20) * cos(π/10)
Дальше осталось посчитать и перемножить значения косинусов.
Советую вам поискать "тригонометрические формулы суммы и разности" также "умножения и деления" они вам ещё пригодятся)
ответ: Все перестановки (1;5;6) , (1;2;3)
Объяснение:
Поскольку левая часть делится на 4, то и правая часть делится на 4.
Число 14- четное, но тогда и число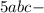
четное
То есть среди чисел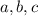
- хотя бы одно четное. Пусть произвольно, в силу симметрии задачи:
Левая часть остается четной, а значит и правая часть должна быть четной, но поскольку 7- нечетное число, то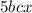
- тоже нечетное число, а значит все числа 
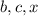- нечетные.
Предположим, что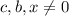
Поделим обе части равенства на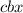
Предположим, что одновременно верно, что :`
Но тогда, в силу того, что все числа целые, а так-же того, что какой бы знак не имели числа x,b,c, всегда хотя бы одно из выражений :
4/c; 2/x ; 4/b ; -7/cbx - отрицательно.
Действительно, если окажется, что -7/сbx > 0 , то хотя бы одно из чисел с,b,x меньше нуля.
Поскольку, число 7/8 - cамое маленькое среди данных 4-x чисел.
То есть мы пришли к противоречию, а значит, хотя бы одно из чисел, a,b,x равно +-1. Тогда в силу симметрии задачи, в уравнении
одно из чисел a,b,c равно либо +-1 либо +-2.
1)
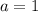
В силу симметрии задачи, все перестановки чисел 1,2,3 и 1,5,6 являются решениями системы.
2)
В других случаях из симметрии так же нет решений.
3)
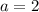
В других случаях так же нет решений.
4)
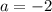
Таким образом больше решений нет.
Осталось рассмотреть: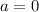
Решений нет.
Примечание: можно было получить разложение сразу для произвольного a, а потом просто подставлять в него различные a. Так было бы немного быстрее и компактнее.
Получено по тому же самому алгоритму, что и в данных примерах.
То есть подставляем : a=+-1 ; +-2; 0 получаем все те же самые случаи.