Кроме этого, известно, что основной период котангенса равен :
Таким образом, аргумент 6 нужно заменить некоторым аргументом вида , чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
Запишем неравенство:
Выполним оценку обеих частей неравенства:
Получим:
Или записывая соотношение для k:
Единственное подходящее целое значение: .
Запишем:
Действительно, , арккотангенс может принимать такое значение.
Смотри) так как уравнение с двумя переменными нужно сделать так чтоб она из переменых в любом случае сократилась,в примере а) и так уже есть переменные которые могут сократиться это х и -х вообщем сладываем получается 3y=6, решаем получаем 2,чтоб узнать y нам нужно подставить х в первое уравнение получаем новое уравнение х+2=4 решаем ответ 2
в примере б) нужно сделать переменную которая должна сократиться это будет y, для этого нам нужно второе уравнение умножить на -2 умножаем и получаем -8х-2y=-6 складываем первое и второе уравнение получаем -3х=6 отсюда х=-2 далее мы подставляем х во второе уравнение и получаем -8+y=3 и находим y решаем и y=11
Известно соотношение:
Кроме этого, известно, что основной период котангенса равен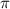 :
:
Таким образом, аргумент 6 нужно заменить некоторым аргументом вида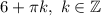 , чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
, чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
Запишем неравенство:
Выполним оценку обеих частей неравенства:
Получим:
Или записывая соотношение для k:
Единственное подходящее целое значение: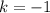 .
.
Запишем:
Действительно, , арккотангенс может принимать такое значение.
, арккотангенс может принимать такое значение.
ответ: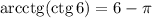
в примере б) нужно сделать переменную которая должна сократиться это будет y, для этого нам нужно второе уравнение умножить на -2 умножаем и получаем -8х-2y=-6 складываем первое и второе уравнение получаем -3х=6 отсюда х=-2 далее мы подставляем х во второе уравнение и получаем -8+y=3 и находим y решаем и y=11