Пусть в сектор вписан прямоугольник . и - середины сторон и соответственно. Так как прямоугольник симметричен оси симметрии сектора, то две его стороны перпендикулярны этой оси, а две другие стороны - параллельны этой оси.
Так как прямоугольник симметричен оси симметрии сектора, то:
Проведем луч , составляющий с осью симметрии сектора угол . Зададим ограничения на х:
Найдем сторону прямоугольника, перпендикулярную оси симметрии сектора.
Рассмотрим треугольник . Запишем соотношение для синуса угла х:
Заметим, что соответствует радиусу сектора. Тогда, выражение для примет вид:
Так как - половина стороны , то найдена первая сторона прямоугольника:
Найдем сторону прямоугольника, параллельную оси симметрии сектора. Представим ее длину в виде:
Длину найдем из того же прямоугольного треугольника , записав выражение для косинуса угла :
Выражаем :
Длину найдем из прямоугольного треугольника . Запишем выражение для тангенса угла :
Откуда:
Так как , то:
Таким образом, найдена вторая сторона прямоугольника:
Площадь прямоугольника равна произведению его смежных сторон:
Найдем производную:
Приравняем производную к нулю:
Учитывая ограничения получим, что:
Проверим, является ли эта точка точкой экстремума.
Найдем значение производной при :
Найдем значение производной при :
При переходе через точку производная меняет знак с плюса на минус. Значит, это точка максимума.
Пусть в сектор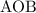 вписан прямоугольник
вписан прямоугольник 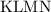 .
. 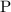 и
и  - середины сторон
- середины сторон 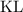 и
и  соответственно. Так как прямоугольник симметричен оси симметрии сектора, то две его стороны перпендикулярны этой оси, а две другие стороны - параллельны этой оси.
соответственно. Так как прямоугольник симметричен оси симметрии сектора, то две его стороны перпендикулярны этой оси, а две другие стороны - параллельны этой оси.
Так как прямоугольник симметричен оси симметрии сектора, то:
Проведем луч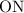 , составляющий с осью симметрии сектора угол
, составляющий с осью симметрии сектора угол  . Зададим ограничения на х:
. Зададим ограничения на х: ![x\in[0;\ \alpha ]](/tpl/images/1361/0024/bc17d.png)
Найдем сторону прямоугольника, перпендикулярную оси симметрии сектора.
Рассмотрим треугольник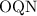 . Запишем соотношение для синуса угла х:
. Запишем соотношение для синуса угла х:
Заметим, что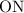 соответствует радиусу сектора. Тогда, выражение для
соответствует радиусу сектора. Тогда, выражение для 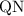 примет вид:
примет вид:
Так как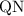 - половина стороны
- половина стороны  , то найдена первая сторона прямоугольника:
, то найдена первая сторона прямоугольника:
Найдем сторону прямоугольника, параллельную оси симметрии сектора. Представим ее длину в виде:
Длину найдем из того же прямоугольного треугольника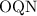 , записав выражение для косинуса угла
, записав выражение для косинуса угла  :
:
Выражаем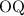 :
:
Длину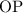 найдем из прямоугольного треугольника
найдем из прямоугольного треугольника 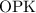 . Запишем выражение для тангенса угла
. Запишем выражение для тангенса угла 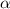 :
:
Откуда:
Так как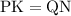 , то:
, то:
Таким образом, найдена вторая сторона прямоугольника:
Площадь прямоугольника равна произведению его смежных сторон:
Найдем производную:
Приравняем производную к нулю:
Учитывая ограничения![x\in[0;\ \alpha ]](/tpl/images/1361/0024/bc17d.png) получим, что:
получим, что:
Проверим, является ли эта точка точкой экстремума.
Найдем значение производной при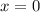 :
:
Найдем значение производной при :
:
При переходе через точку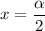 производная меняет знак с плюса на минус. Значит, это точка максимума.
производная меняет знак с плюса на минус. Значит, это точка максимума.
Найдем значение максимума:
Значит, наибольшая площадь прямоугольника равна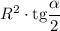
ответ: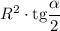
Объяснение:
задача:
В первом ящике 25% от общего числа составляют красные карандаши,
а во втором 1/6 часть -это красные карандаши.
Если все карандаши высыпать в один ящик,
то красные карандаши будут составлять 20% от общего числа всех карандашей.
На сколько процентов меньше карандашей во втором ящике по сравнению с первым?
пусть (а) карандашей в первом ящике, тогда красных карандашей в первом ящике (0.25*а) или (а/4)
пусть (b) карандашей во втором ящике, тогда красных карандашей во втором ящике (b/6)
Если все карандаши высыпать в один ящик (a+b), то красных карандашей будет (0.20*(а+b)) или (а+b)/5
получили уравнение: (а/4) + (b/6) = (а+b)/5
умножим обе части равенства на 60:
15*a + 10*b = 12*a + 12*b
3a = 2b --> b = 1.5a во втором ящике БОЛЬШЕ карандашей (!!)... на 50%
возможно, в условии опечатка...