(x + 4) (x² + x − 13) - (x + 7) (x² + 2x - 5) = x + 1.
х^3+х^2-13х+4х^2+4х-52-х^3-2х^2+5х-7х^2-14х+35=х+1
-4х^2-19х-18=0
D=361-16×18=73
x1=(19-|/73)/(-8)=(|/73-19)/8
x2=(19+|/73)/(-8)=-(|/73+19)/8
Корнями уравнения являются дроби:
Объяснение:
(x + 4)(x² + x - 13) - (x + 7)(x² + 2x - 5) = x + 1
(x³ + x² - 13x + 4x² + 4x - 52) - (x³ + 2x² - 5x + 7x² + 14x - 35) - x - 1 = 0
x³ + 5x² - 9x - 52 - x³ - 9x² - 9x + 35 - x - 1 = 0
-4x² - 19x - 18 = 0 | *(-1)
4x² + 19x + 18 = 0
D = b² - 4*a*c. D = 361 - 288 = 73
x₁ = (-b - √D) / 2a = (-19 - √73) / 8
x₂ = (-b + √D) / 2a = (-19 + √73) / 8)
ответ:
(x + 4) (x² + x − 13) - (x + 7) (x² + 2x - 5) = x + 1.
х^3+х^2-13х+4х^2+4х-52-х^3-2х^2+5х-7х^2-14х+35=х+1
-4х^2-19х-18=0
D=361-16×18=73
x1=(19-|/73)/(-8)=(|/73-19)/8
x2=(19+|/73)/(-8)=-(|/73+19)/8
Корнями уравнения являются дроби: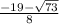


Объяснение:
(x + 4)(x² + x - 13) - (x + 7)(x² + 2x - 5) = x + 1
(x³ + x² - 13x + 4x² + 4x - 52) - (x³ + 2x² - 5x + 7x² + 14x - 35) - x - 1 = 0
x³ + 5x² - 9x - 52 - x³ - 9x² - 9x + 35 - x - 1 = 0
-4x² - 19x - 18 = 0 | *(-1)
4x² + 19x + 18 = 0
D = b² - 4*a*c. D = 361 - 288 = 73
x₁ = (-b - √D) / 2a = (-19 - √73) / 8
x₂ = (-b + √D) / 2a = (-19 + √73) / 8)
ответ: