(x-7)(3x+5)(x-9)< 0, x²-3x+11> 0 будь ласка

Пусть скорость первого велосепедиста одинакова x км/ч. Тогда скорость второго будет одинакова (x+3) км/ч. 1-ый велосепедист проехал всё расстояние одинаковое 36 км за (36/x) часов. 2-ой проехал это расстояние за (36/(x+3)) часов. Известно, что 2-ой велосепедист преодолевает данное расстояние на 1 час прытче.

Составим уравнение:

36/x-36/(x+3)=1

36(x+3)-36x=x(x+3)

36x+108-36x=x^2+3x

x^2+3x-108=0

D=9+4*108=441 sqrtD=21

x1=(-3+21)/2=9

x2=(-3-21)/2=-12lt;0 не подходит

2) 9+3=12(км/ч)

ответ: Скорость первого велосепедиста равна 9 км/ч, а второго- 12 км/ч.

r=3.

Объяснение:

1) Так как трапеция ABCD равнобокая и в неё вписана окружность, то её боковые стороны будут равны средней линии трапеции, т.е. AB=CD=m, где m=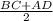==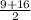12,5. ⇒ AB=CD=12,5.

2) Проведём из точек В и С перпендикуляры к стороне AD. ⇒ BH₁=CH ⇒ AH₁=HD=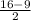=3,5.

3) Рассмотрим прямоугольный треугольник ABH₁. И по теореме Пифагора найдём высоту трапеции ABCD, т.е. BH₁. ⇒

⇒ BH₁=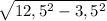==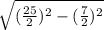==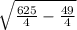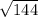12.

4) Площадь трапеции равна S=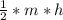, где m - сред.линия; h - высота трапеции. ⇒ S=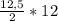=6,25*12=75.

5) Так как в трапецию вписана окружность, то её площадь равна S=pr, где p - полупериметр трапеции; r - радиус вписанной окружности.

⇒ p=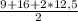=25. ⇒ 75=25*r ⇒ r=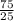=3.