Разделим на :
Замена:
Получим уравнение:
Чтобы найти интеграл, стоящий в левой части, подынтегральную дробь представим в виде суммы составляющих:
Дроби равны, знаменатели равны. Значит, равны и числители:
Условие равенства:
Значит, дробь раскладывается на составляющие следующим образом:
Возвращаемся к интегрированию:
Для второй дроби выполним подведение под знак дифференциала:
Интегрируем:
Обратная замена:
Разделим на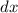 :
:
Разделим на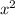 :
:
Замена:
Получим уравнение:
Чтобы найти интеграл, стоящий в левой части, подынтегральную дробь представим в виде суммы составляющих:
Дроби равны, знаменатели равны. Значит, равны и числители:
Условие равенства:
Значит, дробь раскладывается на составляющие следующим образом:
Возвращаемся к интегрированию:
Для второй дроби выполним подведение под знак дифференциала:
Интегрируем:
Обратная замена: