Произведение 3-х множителй делится на любой из своих множителей без остатка.
3*5*11=165 - минимальное 3-х значное число, делящееся на 3, 5 и 11.
Если это число умножить на любое число, это число все равно будет делиться на 3, 5 и 11, так как данные множители остаются и добавляется еще 1.
Ограничения: 3-х значное число и различные цифры. Значит, чтобы получить 3-х значное число, дополнительный множитель может быть не больше, чем 6:
165*6=990 - максимальное 3-х значное число, кратное 3, 5 и 11 одновременно.
Но, при умножении на четные числа от 2 до 6, получаем, соответственно, числа 330, 660 и 990, что выходит за рамки ограницения "различные цифры".
Значит, дополнительные множители, которые можно ввести, это - 3 и 5 (множитель 1 не вводится, потому, что произведение не изменится):
3*5*11*3=495
3*5*11*5=825
ответ: 165; 495; 825
приведем оба уравнения системы к виду y=kx+b(уравнение прямой).
Если две прямые и заданы уравнениями и , то на плоскости они могут быть:
1) и - прямые параллельны, следовательно они не пересекаются и, следовательно, система из таких прямых не имеет решений.
2) и - прямые совпадают, следовательно, система из таких прямых будет иметь бесконечное множество решений.
3) - прямые пересекаются в одной точке, следовательно, система из таких прямых будет иметь только одно решение.
Применим это для решения данной задачи:
Значит, при a=0 данная система не имеет решений.
Значит, при a=3 данная система имеет бесконечное множество решений.
При остальных значениях a система будет иметь только одно решение:
В итоге:
система имеет одно решение.
ответ: a=0 => система не имеет решений(x∈∅)
a=3 => система имеет бесконечное множество решений(x∈R)
a∈(-∞;0)∪(0;3)∪(3;+∞) => система имеет одно решение.
Произведение 3-х множителй делится на любой из своих множителей без остатка.
3*5*11=165 - минимальное 3-х значное число, делящееся на 3, 5 и 11.
Если это число умножить на любое число, это число все равно будет делиться на 3, 5 и 11, так как данные множители остаются и добавляется еще 1.
Ограничения: 3-х значное число и различные цифры. Значит, чтобы получить 3-х значное число, дополнительный множитель может быть не больше, чем 6:
165*6=990 - максимальное 3-х значное число, кратное 3, 5 и 11 одновременно.
Но, при умножении на четные числа от 2 до 6, получаем, соответственно, числа 330, 660 и 990, что выходит за рамки ограницения "различные цифры".
Значит, дополнительные множители, которые можно ввести, это - 3 и 5 (множитель 1 не вводится, потому, что произведение не изменится):
3*5*11*3=495
3*5*11*5=825
ответ: 165; 495; 825
приведем оба уравнения системы к виду y=kx+b(уравнение прямой).
Если две прямые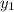
и 
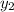заданы уравнениям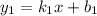и 
и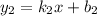 
, то на плоскости они могут быть:
1)
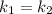и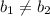 
- прямые параллельны, следовательно они не пересекаются и, следовательно, система из таких прямых не имеет решений.
2)
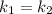и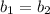 
- прямые совпадают, следовательно, система из таких прямых будет иметь бесконечное множество решений.
3)
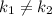- прямые пересекаются в одной точке, следовательно, система из таких прямых будет иметь только одно решение.
Применим это для решения данной задачи:
Значит, при a=0 данная система не имеет решений.
Значит, при a=3 данная система имеет бесконечное множество решений.
При остальных значениях a система будет иметь только одно решение:
В итоге:
ответ: a=0 => система не имеет решений(x∈∅)
a=3 => система имеет бесконечное множество решений(x∈R)
a∈(-∞;0)∪(0;3)∪(3;+∞) => система имеет одно решение.