для каждого числа "b" укажите все значения "а" (а зависит от b), при которых b является точкой указанного вида экстремума данной функции: b - точка минимума
Надо исследовать функцию y, для этого найдем её производную.
График производной - парабола. Нам нужна точка минимума. Очевидно, что нужно знать точки экстремума. Заметим, что парабола всегда направлена вверх. Если парабола находится выше оси ОХ, точек минимума нет. Если касается, учитывая что в исходной функции 6x^3 (на бесконечности возрастает), то будет минимумом. Это условие D≥0
Далее, пусть - точки экстремума. На интервале функция будет убывать, то есть минимума своего достигнет в .
Найдем же эти точки в общем виде:
Теперь же невооруженным глазом видно, что дискриминант всегда больше 0, но докажем это всё-таки: при любых а.
Выразим точки экстремума:
Здесь независимо от значений а точка, где корень взят с "+" будет больше, а значит именно это значение будет точкой минимума.
Теперь подумаем над условием. В таком выражении и будет являться тем самым b. Подбирая любое b, получим выражение через а.
Но нужно ведь выразить а через b. Вернемся к уравнению y'=0
Выражаем а и получаем:
Ну а если через b, то
Но такое соответствие может быть и для точек локальных максимумов. Если значение точки минимума (т.е. то, что с "+" бралось) начать преобразовывать к удобоваримому виду, мы и получим уравнение y'=0, вот начало преобразований:
Уравнение вида
Вот как раз для точки минимума условие g(x)≥0 обязательно.
Вот надо решить это неравенство:
Ищем нули функции
В числителе
Раз D<0, то все выражение больше нуля из-за коэффициента при старшей степени, можно на него поделить без потерь и получить:
А х здесь это b.
То есть при
, где b - точка минимума.
А в остальных случаях для b значение a ему не будет соответствовать как то значение, где b - точка минимума.
Как-то. P.S. странное немного задание, может, я чего-то не понял))
Надо исследовать функцию y, для этого найдем её производную.
График производной - парабола. Нам нужна точка минимума. Очевидно, что нужно знать точки экстремума. Заметим, что парабола всегда направлена вверх. Если парабола находится выше оси ОХ, точек минимума нет. Если касается, учитывая что в исходной функции 6x^3 (на бесконечности возрастает), то будет минимумом. Это условие D≥0
Далее, пусть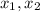 - точки экстремума. На интервале
- точки экстремума. На интервале 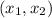 функция будет убывать, то есть минимума своего достигнет в
функция будет убывать, то есть минимума своего достигнет в 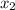 .
.
Найдем же эти точки в общем виде:
Теперь же невооруженным глазом видно, что дискриминант всегда больше 0, но докажем это всё-таки: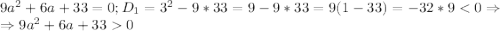 при любых а.
при любых а.
Выразим точки экстремума:
Здесь независимо от значений а точка, где корень взят с "+" будет больше, а значит именно это значение будет точкой минимума.
Теперь подумаем над условием. В таком выражении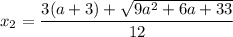 и будет являться тем самым b. Подбирая любое b, получим выражение через а.
и будет являться тем самым b. Подбирая любое b, получим выражение через а.
Но нужно ведь выразить а через b. Вернемся к уравнению y'=0
Выражаем а и получаем:
Ну а если через b, то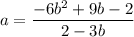
Но такое соответствие может быть и для точек локальных максимумов. Если значение точки минимума (т.е. то, что с "+" бралось) начать преобразовывать к удобоваримому виду, мы и получим уравнение y'=0, вот начало преобразований:
Уравнение вида
Вот как раз для точки минимума условие g(x)≥0 обязательно.
Вот надо решить это неравенство:
Ищем нули функции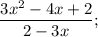
В числителе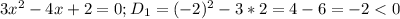
Раз D<0, то все выражение больше нуля из-за коэффициента при старшей степени, можно на него поделить без потерь и получить:
А х здесь это b.
То есть при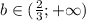
А в остальных случаях для b значение a ему не будет соответствовать как то значение, где b - точка минимума.
Как-то. P.S. странное немного задание, может, я чего-то не понял))