Теорема Виета гласит, что произведение корней приведенного квадратного уравнения равно свободному члену (q), а их сумма равна числу обратному второму коэффициенту (-p)
x₁ · x₂ = q
x₁ + x₂ = -p
Часто нам будут даваться не приведенные квадратные уравнение, а обычные, они имеют вид
ax² + bx + c = 0 (то же приведенное, но с коэффициентом перед x-ом)
что бы получить из обычного квадратного уравнение приведенное, нужно разделить его на a. От сюда сумма и произведение корней обычного квадратного уравнения равны:
Решение a) Пусть ε > 0. Требуется поэтому ε найти такое δ > 0, чтобы из условия 0 < |x − x0| < δ, т.е. из 0 < |x - 0| < δ вытекало бы неравенство |f(x) − A| < ε, т.е. |3x - 2 − (- 2)| < ε. Последнее неравенство приводится к виду |3(x )| < ε, т.е. |x | < (1/3)* ε. Отсюда следует, что если взять δ = ε/3 , то неравенство 0 < |x | < δ будет автоматически влечь за собой неравенство |3x - 2 − (- 2)| < ε. По определению это и означает, что lim x→ −2 (3x - 2) = −2
Коли просите, не могу отказать ;) Я дам только решение, без доказательств и тонкостей, все это можно найти в интернете при должном желании.
x² + px + q = 0 - приведенное квадратное уравнение
Теорема Виета гласит, что произведение корней приведенного квадратного уравнения равно свободному члену (q), а их сумма равна числу обратному второму коэффициенту (-p)
x₁ · x₂ = q
x₁ + x₂ = -p
Часто нам будут даваться не приведенные квадратные уравнение, а обычные, они имеют вид
ax² + bx + c = 0 (то же приведенное, но с коэффициентом перед x-ом)
что бы получить из обычного квадратного уравнение приведенное, нужно разделить его на a. От сюда сумма и произведение корней обычного квадратного уравнения равны:
x₁ · x₂ =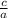
x₁ + x₂ = -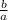
Пример:
x² - 4x + 3 = 0
Тогда корни:
x₁ = 1
x₂ = 3
Надеюсь, что все понятно)
a) Пусть ε > 0. Требуется поэтому ε найти такое δ > 0, чтобы
из условия 0 < |x − x0| < δ, т.е. из 0 < |x - 0| < δ
вытекало бы неравенство |f(x) − A| < ε, т.е. |3x - 2 − (- 2)| < ε.
Последнее неравенство приводится к виду |3(x )| < ε, т.е. |x | < (1/3)* ε. Отсюда следует, что если взять δ = ε/3 , то неравенство 0 < |x | < δ
будет автоматически влечь за собой неравенство |3x - 2 − (- 2)| < ε.
По определению это и означает, что lim x→ −2 (3x - 2) = −2