Примем производительность первого маляра за х, второго за у Тогда вдвоем они за 1 час покрасят х+у=40 м² Работая в одиночку, первый маляр покрасит 50 м² за 50:х (часов) а второй 90м² за 90:у (часа) Из условия задачи известно, что 90:у-50:х=4 (часа) Составим систему уравнений: |х+у=40 |90:у-50:х=4 Из первого уравнения найдем у через х у=40-х Подставим это значение во второе уравнение
90:(40-х)-50:х=4 Умножим обе части уравнения на х(40-х), чтобы избавиться от дроби. 90х-50(40-х)=4 х(40-х), 90х-2000 +50х =160х -4х² 4х² +90х-2000 +50х - 160х= 0 4х² -20х-2000=0 Для облегчения вычисления разделим обе части на 4, получим х² -5х-500=0
Слова "пересечение с осями координат" означают, что нужно положить одну координату равной нулю (это ситуация соответствует пересечению с другой осью) и найти из получившегося уравнения оставшуюся неизвестную, затем провести аналогичную операцию со второй координатой (пересечение с другой осью).
Например, рассмотрим равенство . Чтобы определить в какой точке график такой функции пересекает абсциссу (ось х), нужно положить . Тогда получим, что , значит пересечение с осью x происходит в точке . Аналогично для оси ординат.
Если вы не представляете себе, как выглядит график линейной функции, попробуйте построить его по точкам.
Примем производительность первого маляра за х, второго за у
Тогда вдвоем они за 1 час покрасят
х+у=40 м²
Работая в одиночку, первый маляр покрасит 50 м² за
50:х (часов)
а второй 90м² за
90:у (часа)
Из условия задачи известно, что
90:у-50:х=4 (часа)
Составим систему уравнений:
|х+у=40
|90:у-50:х=4
Из первого уравнения найдем у через х
у=40-х
Подставим это значение во второе уравнение
90:(40-х)-50:х=4 Умножим обе части уравнения на х(40-х), чтобы избавиться от дроби.
90х-50(40-х)=4 х(40-х),
90х-2000 +50х =160х -4х²
4х² +90х-2000 +50х - 160х= 0
4х² -20х-2000=0 Для облегчения вычисления разделим обе части на 4, получим
х² -5х-500=0
Решая задачу через дискриминант, получим
х=25 м² в час
100 м² первый маляр покрасит за
100:25=4 часа.
Слова "пересечение с осями координат" означают, что нужно положить одну координату равной нулю (это ситуация соответствует пересечению с другой осью) и найти из получившегося уравнения оставшуюся неизвестную, затем провести аналогичную операцию со второй координатой (пересечение с другой осью).
Например, рассмотрим равенство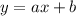
. Чтобы определить в какой точке график такой функции пересекает абсциссу (ось х), нужно положить 
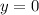. Тогда получим, что 
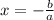, значит пересечение с осью x происходит в точке 
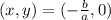. Аналогично для оси ординат.
Если вы не представляете себе, как выглядит график линейной функции, попробуйте построить его по точкам.