Я не хочу погибнуть от математики омг, уже поздно
—
написать уравнение касательной, проведённой к графику функции
f(x)=x^2+2x–8 в точке с абсциссой это надо сдать​

Какая из точек А( 8 ; 0 ) , В ( -2 ; 3) , С( -2 ; 5 ) и D( 2 ; 5) лежит на графике функции у = - 0,5х+4? Постройте график этой линейной функции .

РЕШЕНИЕ:

Чтобы определить, какая из данных точек лежит на графике функции у = - 0,5х + 4, необходимо подставить координаты этих точек (  Е ( х ; у )  )  в заданную функцию, получаем:

A( 8 ; 0 ) :
0 = - 0,5 • 8 + 4
0 = - 4 + 4
0 = 0   =>  точка А( 8 ; 0 ) принадлежит графику функции

B( - 2 ; 3 ) :
3 = - 0,5 • ( - 2 ) + 4
3 = 1 + 4
3 = 5   =>  точка  В( - 2 ; 3 ) не принадлежит графику функции

С( - 2 ; 5 ) :
5 =  - 0,5 • ( - 2 ) + 4
5 = 1 + 4
5 = 5  =>  точка  С( - 2 ; 5 ) принадлежит графику функции

D( 2 ; 5 ) :
5 = - 0,5 • 2 + 4
5 = - 1 + 4
5 = 3  =>  точка  D( 2 ; 5 ) не принадлежит графику функции

Итак, точки, лежащие на графике функции у = - 0,5х+4 : А( 8 ; 0 ) и С( - 2 ; 5 )

• График линейной функции у = - 0,5х + 4 показан в приложении •

прощения, но решение получилось слишком сложным :(

 

q - знаменатель геом. прогр.

d - сумма арифм. прогрессии

 

a - первый член ар. прогр.

b - первый член геом. прогр.

 

1) a+d+a+2d=2a+3d=12;  также b+bq=b(1+q)=12; также bq+a+d=12 

2) a+2d=bq

3) a+d=b

4) a+bq^2=14

 

из b(1+q)=12:

 

из a+2d=bq и a+d=b выражаем b+d=bq -> d=bq-b=b(q-1)

 

т.е.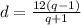  

 

из a+bq^2=14 выразим a=14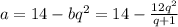 

 

Подставим в 2a+3d=12 получим квадратное уравнение вида:

 

 

После всех приведений и сокращений и с учетом, что занменатель д.б. не равен 0, получим:

 

 

Решая єто уравнения получим, что q=5/3 - не подходит, т.к. в условии числа д.б. целыми и q=1/2.

 

Отсюда b=8, a=12, d=-4

 

Получаем последовательность:

 

12   8   4   2