Я ЗА РЕШЕНИЕ 1. Определите вид последовательности и найдите первые три значения
А) a1=3 an=2(an-1)2 – 1
Б) аn =5n2-2
B) утроенное значение делится на 4
2. Найдите 25й член арифметической прогрессии и S10, если она состоит из чисел 17,20,23,… .
3. В геометрической прогрессии b4=24, b6=96. Найти q и b1
4. Найдите b1.если S= 3/8 q=1/3

Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)

Решим к примеру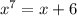 уравнение в действительных корнях.

Рассмотрим функцию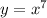 . Эта функция является возрастающей на всей числовой прямой.

Также рассмотрим правую часть уравнения: функцию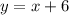 . Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).

графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.

Возьмем теперь к примеру уравнение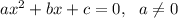 

Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.

Если D=0, то квадратное уравнение имеет два равные корни.

Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.

ответ:иррациональное

Объяснение:

Пусть √28 + 10√3 рациональное

√28 + 10√3=√4*7+10√3=2√7+10√3=2(√7+5√3)-рациональное

2 рациональное, значит √7+5√3 рациональное.

возведем в квадрат (√7+5√3)^2=7+2*5√3*7+25*3=7+10*√21+75=82+10*√21

√7+5√3 рациональное значит, √7+5√3 в квадрате тоже рациональное.

Значит 82+10*√21 рациональное, 82 рациональное => 10*√21, тоже рациональное.

10 рациональное значит √21 рациональное ПРОТИВОРЕЧИЕ

значит√28 + 10√3 иррациональное

(если что мы предполагали что √28 + 10√3 рациональное)