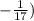Яка з пар чисел (-2; 3), (2; 3), (-2; -3),

(2; -3) є розв’язками рівняння 7х – 5у = - 1?​

ответ: 1) x = 10-3y

2) y = 5x-2

3) x = 4-3y

4) x = 5/6y-2/3

Объяснение: 1) Выражаем x через y, значит оставляем в левой части только x, переносим всё в правую часть уравнения. 3y переносим через знак "равно", значит меняем + на -, 10 оставляем.

2) Выражаем y через x, значит оставляем в левой части только y, переносим всё в правую часть уравнения. Перенесём 5x вправо, у нас изменится знак на "-", получаем -y = -5x+2, домножим уравнение на "-1" и получим y = 5x-2

3) Выражаем x через y, значит оставляем в левой части только x, переносим всё в правую часть уравнения. После переноса получаем 2x = 8-6y, разделим обе части уравнения на 2 и получим x = 4-3y

4) Выражаем x через y, значит оставляем в левой части только x, переносим всё в правую часть уравнения. После переноса получаем 6x = 5y-4. Разделим обе части уравнения на 6 и получим x = 5/6y-4/6 или же x = 5/6y - 2/3

ответ: 4

Я решил все намного подробнее, но у меня полетел сайт. Расписывать я не буду, извини...

1) Приведем дроби в правой части неравенства к общему знаменателю:

2) Умножим обе части неравенства на 6:

3) Отнимем из обеих частей неравенства 6 и прибавим x:

4) Разделим обе части неравенства на -17, при этом его знак поменяется на противоположный:

5) Отметим эту точку на координатной прямой и заштрихyем область, которая левее -1/17 согласно условию "нового" неравенства (x < -1/17)

6) Так, решением неравенства являются все точки, принадлежащие промежутку (-∞;