Является ли функция f(x)=2x-x+3sinpx непрерывной в точке x=3?

Перепишем функцию в виде уравнения:

Воспользуемся уравнением для пучка прямых, проходящих через заданную точку для того, чтобы найти угловой коэффициент и точку пересечения с осью Y.
Вид уравнения с угловым коэффициентом: , где  равняется угловому коэффициенту, а  равняется координате  пересечения прямой с осью Y:

Находим значения  и  с формы :


Угловым коэффициентом прямой является значение , а координатой Y пересечения с осью Y является значение .
Угловой коэффициент - 
Ордината пересечения с осью Y: 

1 )

Построим график функции y = x³.

Заметим, что график функции будет пересекать ось абсцисс и ось ординат в точке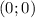 (это несложно определить, решив два уравнения 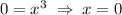и 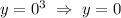), а также определен при всех значениях действительных значения аргумента .

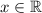Теперь можем определить несколько дополнительных точек (при желании, это можно было сделать и сразу):

Далее проводим через все эти точки плавную линию, как показано на  чертеже в приложении.

График построен!

2 )

Функция четная или нечетная?

По построенному только что графику видно, что он симметричен относительно начала координат. Это означает, что рассматриваемая функция - нечетная (ведь если график симметричен относительно начала координат, то функция нечетная, а если симметричен относительно оси абсцисс, то нечетная).

Это можно было определить и аналитически. Как известно, если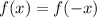 , то функция четная, а если 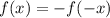, то нечетная (в противном случае функция свойством четности не обладает).

При этом .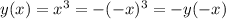

Так или иначе, получаем, что функция нечетная.

3 )

Принадлежат ли точки графику?

а)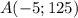   . НЕ принадлежит.

б)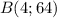   . Принадлежит.

в)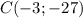   . Принадлежит.

То есть графику принадлежат только точки B и C.