a) Возрастает: (-∞;0)∪(2/3;∞), убывает: (0;2/3)
б) 0 - локальный максимум, 2/3 - минимум
в) Наибольшее y=52 при x=4, наименьшее: y=4 при x=1
Объяснение:
Производная равна: . Отсюда x1=0, x2=2/3. Это точки экстремума.
б)
0 - максимум
2/3 - минимум
а)
На основании максимума и минимума получаем:
Функция возрастает (-∞;0)∪(2/3;∞)
Функция убывает (0;2/3)
в)
На всем промежутке от 1 до 4 функция возрастает, поэтому наименьшее значение y=4 находится при x=1, а наибольшее y=52 находится при x=4.
Нужно просто подставить 1 и 4 в функцию вместо x, чтобы вычислить y.
a) Возрастает: (-∞;0)∪(2/3;∞), убывает: (0;2/3)
б) 0 - локальный максимум, 2/3 - минимум
в) Наибольшее y=52 при x=4, наименьшее: y=4 при x=1
Объяснение:
Производная равна: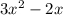 . Отсюда x1=0, x2=2/3. Это точки экстремума.
. Отсюда x1=0, x2=2/3. Это точки экстремума.
б)
0 - максимум
2/3 - минимум
а)
На основании максимума и минимума получаем:
Функция возрастает (-∞;0)∪(2/3;∞)
Функция убывает (0;2/3)
в)
На всем промежутке от 1 до 4 функция возрастает, поэтому наименьшее значение y=4 находится при x=1, а наибольшее y=52 находится при x=4.
Нужно просто подставить 1 и 4 в функцию вместо x, чтобы вычислить y.
Для этого мы применим правило умножения скобки на скобку и получим следующее уравнение:
(2x - 3)(4x + 3) - 8x2 = 33;
2x * 4x + 2x * 3 - 3 * 4x - 3 * 3 - 8x2 = 33;
8x2 + 6x - 12x - 9 - 8x2 = 33;
Перенесем -9 в правую часть уравнения и сменим его знак на противоположный:
8x2 - 8x2 + 6x - 12x = 33 + 9;
-6x = 42;
Ищем неизвестный множитель:
x = 42 : (-6);
x = -7.
Ответ: x = -7 решение уравнение