Сразу обозначим собственную скорость корабля за . Тогда:
скорость корабля по течению равна км/ч;а против течения: км/ч.
Заметим, что за то время, пока корабль успел проплыть туда-сюда, бревно лишь проплыло км со скоростью км/ч (за скорость бревна мы принимаем скорость реки, так как подразумеваем, что никаких людей или моторчика на бревне не предусмотрено).
Значит, время движения бревна равно часов.
И еще:
по течению корабль плыл часов;а против течения: .
Так как бревно и корабль двигались одинаковое время, то мы можем дальше только составить уравнение и решить его:
Первый корень не сказать, чтобы нам подходит, а второй корень - в самый раз! Он не только правдоподобный, но и не дает нуля в знаменателе!
Отмечаем решения первого и второго неравенства на числовой оси и находим пересечение решений (решение, которое подходит и первому, и второму неравенству).
Такое решение х∈(-4/3, -9/20)
2)(х-1)/2<1
4-x>(x-5)/3
Избавляемся от дроби: первое уравнение умножаем на 2, второе уравнение умножаем на 3:
x-1<2
12-3х>x-5
x<3 х∈(-∞, 3)
-3x-x> -5-12
-4x> -17
x<-17/-4
x<4,25 х∈(-∞, 4,25)
Отмечаем решения первого и второго неравенства на числовой оси и находим пересечение решений (решение, которое подходит и первому, и второму неравенству).
Сразу обозначим собственную скорость корабля за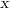 . Тогда:
. Тогда:
скорость корабля по течению равнаЗаметим, что за то время, пока корабль успел проплыть туда-сюда, бревно лишь проплыло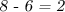 км со скоростью
км со скоростью 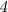 км/ч (за скорость бревна мы принимаем скорость реки, так как подразумеваем, что никаких людей или моторчика на бревне не предусмотрено).
км/ч (за скорость бревна мы принимаем скорость реки, так как подразумеваем, что никаких людей или моторчика на бревне не предусмотрено).
Значит, время движения бревна равно часов.
часов.
И еще:
по течению корабль плылТак как бревно и корабль двигались одинаковое время, то мы можем дальше только составить уравнение и решить его:
Первый корень не сказать, чтобы нам подходит, а второй корень - в самый раз! Он не только правдоподобный, но и не дает нуля в знаменателе!
Задача решена!
ответ:1) х∈(-4/3, -9/20)
2) х∈(-∞, 3)
Объяснение:
1)2х+7>3-x
x/3-1>2x-1/4
2x+x>3-7
x/3-2x> -1/4+1
3x> -4
-5/3x>3/4
x> -4/3 х∈(-4/3, ∞)
x< -9/20 х∈(-∞, -9/20)
Отмечаем решения первого и второго неравенства на числовой оси и находим пересечение решений (решение, которое подходит и первому, и второму неравенству).
Такое решение х∈(-4/3, -9/20)
2)(х-1)/2<1
4-x>(x-5)/3
Избавляемся от дроби: первое уравнение умножаем на 2, второе уравнение умножаем на 3:
x-1<2
12-3х>x-5
x<3 х∈(-∞, 3)
-3x-x> -5-12
-4x> -17
x<-17/-4
x<4,25 х∈(-∞, 4,25)
Отмечаем решения первого и второго неравенства на числовой оси и находим пересечение решений (решение, которое подходит и первому, и второму неравенству).
Такое решение х∈(-∞, 3)