З пункту А в пункт В між якими 80км, одночасно назустріч один одному виїхали два велосипедисти. Після зустрічі перший велосипедист прибуває у В через 1 год 20 хв, а другий в А через 3 год. З якою швидкість їхали велосипедисти?
Припустимо, що перший велосипедист має швидкість - х, та він проїхав до місця зустрічі С км. ( на це йому потрібно С / х часу ), після зістрічі він проїхав ( 80 - С ) км. за 1 годину та 20 хвилин.
Другий велосипедист має швидкість - у, та він проїхав до місця зустрічі ( 80 - С ) км. ( на це йому потрібно ( 80 - С ) / у часу ), після зустрічі він проїхав С км. за 3 години.
До місця зустрічі обидва велосипедисти їхали однакову кількість часу.
С / х = ( 80 - С ) / у
С / х - ( 80 - С ) / у = 0 (1)
( 80 - С ) / х = 4 / 3 ( 1 година 20 хвилин ).
х = ( 80 - С ) × 3 / 4 (2)
С / у = 3 ( 3 години ).
у = С / 3 (3)
Подставимо (2) та (3) до (1).
4 × С / ( 3 × ( 80 - С ) ) - 3 × ( 80 - С ) / С = 0
4С^2 - 9 × ( 80 - С ) × ( 80 - С ) = 0
4С^2 - 9 × 80^2 + 9 × 160 × С - 9С^2 = 0
5С^2 - 1440С + 57600 = 0
D = 1440^2 - 4 × 5 × 57 600 = 921600
С1 = ( 1440 + 960 ) / 10 = 240 км.
С2 = ( 1440 - 960 ) / 10 = 48 км.
Перший корінь ми відкидаємо, бо частина дістанції не може бути більшою за всю дістанцію, а 240 > 80.
С = 48 км. - відстань, що проїхав перший велосипедист до місця зустріці з другим.
80 - 48 = 32 км. - відстань, що проїхав другий велосипедист до зустрічі з першим.
Підставимо С до (2) та (3).
х = ( 80 - 48 ) × 3 / 4 = 32 × 3 / 4 = 24 км/год.
у = 48 / 3 = 16 км/год.
Перевірка.
48 / 24 = ( 80 - 48 ) / 16 = 32 / 16
2 = 2 - велосипедисти їхали 2 години до місця зустрічі.
Расстояние между ними 80 км пусть скорость первого велосипедиста а второго из чертежа нам известно что 1) и так же мы знаем что 2) 3) приравняем 3) и 4) уравнения мы знаем что подставим в это уравнение и выйдет подставим t во второе и третье уравнение тогда выйдет ; ответ: скорость первого велосипедиста 24 км/ч ; а скорость второго 16км/ч
Відповідь:
Швидкість першого велосипедиста 24 км/год.
Швидкість другого велосипедиста 16 км/год.
Пояснення:
Припустимо, що перший велосипедист має швидкість - х, та він проїхав до місця зустрічі С км. ( на це йому потрібно С / х часу ), після зістрічі він проїхав ( 80 - С ) км. за 1 годину та 20 хвилин.
Другий велосипедист має швидкість - у, та він проїхав до місця зустрічі ( 80 - С ) км. ( на це йому потрібно ( 80 - С ) / у часу ), після зустрічі він проїхав С км. за 3 години.
До місця зустрічі обидва велосипедисти їхали однакову кількість часу.
С / х = ( 80 - С ) / у
С / х - ( 80 - С ) / у = 0 (1)
( 80 - С ) / х = 4 / 3 ( 1 година 20 хвилин ).
х = ( 80 - С ) × 3 / 4 (2)
С / у = 3 ( 3 години ).
у = С / 3 (3)
Подставимо (2) та (3) до (1).
4 × С / ( 3 × ( 80 - С ) ) - 3 × ( 80 - С ) / С = 0
4С^2 - 9 × ( 80 - С ) × ( 80 - С ) = 0
4С^2 - 9 × 80^2 + 9 × 160 × С - 9С^2 = 0
5С^2 - 1440С + 57600 = 0
D = 1440^2 - 4 × 5 × 57 600 = 921600
С1 = ( 1440 + 960 ) / 10 = 240 км.
С2 = ( 1440 - 960 ) / 10 = 48 км.
Перший корінь ми відкидаємо, бо частина дістанції не може бути більшою за всю дістанцію, а 240 > 80.
С = 48 км. - відстань, що проїхав перший велосипедист до місця зустріці з другим.
80 - 48 = 32 км. - відстань, що проїхав другий велосипедист до зустрічі з першим.
Підставимо С до (2) та (3).
х = ( 80 - 48 ) × 3 / 4 = 32 × 3 / 4 = 24 км/год.
у = 48 / 3 = 16 км/год.
Перевірка.
48 / 24 = ( 80 - 48 ) / 16 = 32 / 16
2 = 2 - велосипедисти їхали 2 години до місця зустрічі.
Расстояние между ними 80 км пусть скорость первого велосипедиста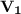
а второго 
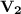из чертежа нам известно что 1) 
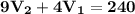и так же мы знаем что 2) 
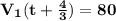3) 
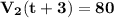
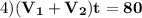приравняем 3) и 4) уравнения 
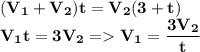мы знаем что 
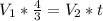подставим в это уравнение и выйдет 
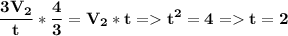подставим t во второе и третье уравнение тогда выйдет 
; 
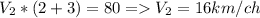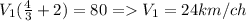ответ: скорость первого велосипедиста 24 км/ч ; а скорость второго 16км/ч