За круглим столом сидять 2021 людина, кожний з яких або лицар, тобто завжди каже правду, або брехун, який кожного разу бреше. Їм роздали по одній картці. На кожній з карток написане по одному числу, при цьому усі числа на картках різні. Глянувши на картки сусіда ліворуч та праворуч, кожний з 2021 людини за столом, сказав: «Число на моїй картці більше, ніж у кожного з обох моїх сусідів». Після цього k з 2021 людини за столом сказали: «Моє число менше, ніж у кожного з двох моїх сусідів». При якому найбільшему k це могло статися?

Показать ответ

Ответ:

danchik60

01.01.2020 21:24

Пусть первое число равно x + 5, тогда второе — x – 5 (замечание: x ∈ N и x > 5). Используя данные условия, получаем, что 10^y = (x + 5)(x – 5) + 1, где y ∈ N. x² – 25 + 1 = 10^y ⇔ x² – 24 = 10^y ⇔ x² = 10^y + 24

Рассмотрим два случая.
1. 0 < y < 4.
Нетрудно убедиться, что равенству удовлетворяет только y = 3: x = 32 — тогда искомые числа 27 и 37.

2. y ≥ 4.
В этом случае 8 | x² и 4 | x ⇒ x = 4z, где z ∈ N. Равенство перепишется в 16z² = 10^(y – 3)1000 + 24 ⇔ 2z² = 10^(y – 3)125 + 3
Заметим, что 2z² ≡ 0 (mod 2), 3 ≡ 1 (mod 2), 10^(y – 3)125 ≡ 0 (mod 2) ⇒ решений нет.

Таким образом, таких чисел всего два: 27 и 37. Большее из этих чисел — 37.

ответ: 37.

0,0(0 оценок)

Ответ:

Дарина15746

28.01.2023 09:07

$$ \frac{a^3+b^6}{2}\geq 3ab^2-4;$

Вспоминаем неравенство Коши

$$\frac{a+b}{2}\geq \sqrt{ab}$

Применяем:

$$\frac{a^3+b^6}{2}\geq \sqrt{a^3b^6}=|ab|^3\sqrt{a}=a|b|^3\sqrt{a}, (a0)$

Покажем, что правое выражение здесь не меньше правого выражения в исходном неравенстве, тогда правое выражение в исходном неравенстве тем более будет не меньше, чем левое в исходном.

Это как если надо доказать, что a>b, мы доказали, что при a>c выполняется c>b, то точно a>b (транзитивность неравенств).

Делаем это:

$a|b|^3\sqrt{a}\geq 3ab^2-4; a|b|^3\sqrt{a}-3ab^2+4\geq 0; ab^2(|b|\sqrt{a}-3)+4\geq 0$

Это неравенство аналогично неравенству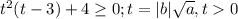 $t^2(t-3)+4\geq 0; t=|b|\sqrt{a}, t0$

Чтобы решить это неравенство, надо найти нули функции

f(t)=t^3-3t^2+4; , здесь сумма коэффициентов при нечетных степенях (1) равна сумме коэффициентов при нечетных степенях (-3+4=1), значит, t=-1 - корень. Поделив уголком на t+1 или по схеме Горнера, получим разложение t^3-3t^2+4=(t+1)(t^2-4t+4)=(t+1)(t-2)^2

Теперь можно решать неравенство, при этом по методу интервалов, так как при t везде коэффициент равен 1, в самом правом промежутке будет "+", а в остальных случаях при переходе через нули будет чередоваться, кроме нулей четности, как здесь t=2 (2-я степень при скобке), знаки будут - + +

Тогда $(t+1)(t-2)^2\geq 0 \Rightarrow t \in[-1;2]\cup[2;+\infty) \Rightarrow t \in [-1;+\infty)$

Но мы рассматриваем только t>0, а там везде неравенство выполняется, значит, выполняется и неравенство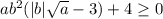 $ab^2(|b|\sqrt{a}-3)+4\geq 0$ , то есть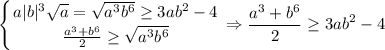 $$\left \{ {{a|b|^3\sqrt{a}=\sqrt{a^3b^6}\geq 3ab^2-4} \atop {\frac{a^3+b^6}{2}\geq \sqrt{a^3b^6} }} \right. \Rightarrow \frac{a^3+b^6}{2} \geq 3ab^2-4$