Найдём уравнение касательных к графику функции f(x) = -8x-x².
f'(x) = -(8x)'-(x²)' = -8-2x
Уравнение для касательной с абсциссой точки касания x₁ = -6:
f'(x₁) = f'(-6) = -8-2·(-6) = -8+12 = 4;
f(x₁) = f(-6) = -8·(-6)-(-6)² = 48-36 = 12;
y = f'(x₁)·(x-x₁)+f(x₁) = 4·(x-(-6))+12 = 4x+24+12 = 4x+36.
Уравнение для касательной с абсциссой точки касания x₂ = 1:
f'(x₂) = f'(1) = -8-2·1 = -8-2 = -10;
f(x₂) = f(1) = -8·1-1² = -8-1 = -9;
y = f'(x₂)·(x-x₂)+f(x₂) = -10·(x-1)+(-9) = -10x+10-9 = -10x+1.
Стороны треугольника лежат на прямых:
y = 4x+36; y = -10x+1; x = 0.
Найдём вершины треугольника.
Сторона AB лежит на оси Oy, поэтому высота CH, треугольника ABC, будет параллельна оси Ox. А значит, CH = |-2,5| = 2,5.
AB = 36-1 = 35, поскольку эта сторона перпендикулярна оси Ох.
Площадь треугольника равна полупроизведению его высоты и стороны к которой она проведена.
S(ABC) = = 2,5·35/2 = 175/4 = 43,75
ответ: 43,75.
Раскладываем с МНК (метода неопределенных коэффициентов)
Знаем, что любое уравнение четвертой степени раскладывается на два квадратных по принципу:
Здесь применяем наше уравнение:
Решаем систему:
Такую систему решаем с подстановки.
Возьмем
Вариантов такого решения несколько. Вот они:
Надо найти такую пару, чтобы она удовлетворяла нашему уравнению!
Итак,
Подставляем его в третье уравнение нашей системы:
Значит, мы имеем:
Для проверки подставим все значения во второе уравнение нашей системы:
Значит, мы верно выбрали пару. Остальные пары нам не подходят.
Все значения подставляем в два квадратных уравнения:
Решаем каждое уравнение в отдельности:
Нет действительных решений.
ответ:
Найдём уравнение касательных к графику функции f(x) = -8x-x².
f'(x) = -(8x)'-(x²)' = -8-2x
Уравнение для касательной с абсциссой точки касания x₁ = -6:
f'(x₁) = f'(-6) = -8-2·(-6) = -8+12 = 4;
f(x₁) = f(-6) = -8·(-6)-(-6)² = 48-36 = 12;
y = f'(x₁)·(x-x₁)+f(x₁) = 4·(x-(-6))+12 = 4x+24+12 = 4x+36.
Уравнение для касательной с абсциссой точки касания x₂ = 1:
f'(x₂) = f'(1) = -8-2·1 = -8-2 = -10;
f(x₂) = f(1) = -8·1-1² = -8-1 = -9;
y = f'(x₂)·(x-x₂)+f(x₂) = -10·(x-1)+(-9) = -10x+10-9 = -10x+1.
Стороны треугольника лежат на прямых:
y = 4x+36; y = -10x+1; x = 0.
Найдём вершины треугольника.
Сторона AB лежит на оси Oy, поэтому высота CH, треугольника ABC, будет параллельна оси Ox. А значит, CH = |-2,5| = 2,5.
AB = 36-1 = 35, поскольку эта сторона перпендикулярна оси Ох.
Площадь треугольника равна полупроизведению его высоты и стороны к которой она проведена.
S(ABC) =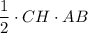 = 2,5·35/2 = 175/4 = 43,75
= 2,5·35/2 = 175/4 = 43,75
ответ: 43,75.