Задача 23.7. 1) Сколько существует выбрать классного руководителя и спортивного респондента из 20 учеников? 2) Сколько существует поставить одну из оценок {3; 4; 5} двум студентам?
Составляем уравнения касательных по формуле y=f(a)+f'(a)(x-a)
f'(x)=4x-3
f'(a)=f'(-1)=4*(-1)-3=-7 f'(2)=4*2-3=5
f(-1)=2+3-1=4 f(2)=8-6-1=1
y=4-7(x+1) y=1+5(x-2)
y=-7x-3 y=5x-9 Это уравнения касательных.
Строим все линии на коорд. плоскости. Видим треугольник , образованный касательными и осью у Две вершины его на оси х: А(-3/7) и В(9/5) находятся из уравнений касательных при у=0..Третья вершинаС-точка пересечения касательных, т.е. 5х-9=-7х-3.
Раскладываем вторую скобку по формуле разности кубов
Заметим, что неполный квадрат в третьей скобке всегда положителен
Докажем это
Так как квадраты не могут быть отрицательными.
Значит можно рассмотреть неравенство методом интервалов.
1) При х<0 первый множитель будет меньше нуля, второй тоже меньше нуля. Два множителя меньше нуля дадут положительное число. А третий будет положительным. Значит все выражение в левой части будет положительным.
2) При Первый множитель будет больше нуля, второй меньше нуля, а третий как всегда положителен. Отрицательный множитель помноженный на положительные множители даст в итоге отрицательное число.
3)
Первый множитель будет положителен, второй тоже положителен. А третий как всегда положителен. Значит в итоге, перемножив три положительных числа, получим положительное число.
В ответе получим два промежутка из первого и третьего случаев.
Заметно, что целочисленных решений будет бесконечно много. Это и все отрицательные целые числа и целые числа большие 2. Так как
Решений, так сказать, счетное множество.
Ну, а если бы был бы в неравенстве противоположный знак, то было бы всего два решения из второго случая. Это числа 1 и 2.
Составляем уравнения касательных по формуле y=f(a)+f'(a)(x-a)
f'(x)=4x-3
f'(a)=f'(-1)=4*(-1)-3=-7 f'(2)=4*2-3=5
f(-1)=2+3-1=4 f(2)=8-6-1=1
y=4-7(x+1) y=1+5(x-2)
y=-7x-3 y=5x-9 Это уравнения касательных.
Строим все линии на коорд. плоскости. Видим треугольник , образованный касательными и осью у Две вершины его на оси х: А(-3/7) и В(9/5) находятся из уравнений касательных при у=0..Третья вершинаС-точка пересечения касательных, т.е. 5х-9=-7х-3.
х=0,5
у=5*0,5-9=-6,5 Н=6,5-высота треугольника. S=2*(1/2 (9/5+3/7)*6/5=
Раскладываем вторую скобку по формуле разности кубов
Заметим, что неполный квадрат в третьей скобке всегда положителен
Докажем это
Так как квадраты не могут быть отрицательными.
Значит можно рассмотреть неравенство методом интервалов.
1) При х<0 первый множитель будет меньше нуля, второй тоже меньше нуля. Два множителя меньше нуля дадут положительное число. А третий будет положительным. Значит все выражение в левой части будет положительным.
2) При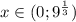 Первый множитель будет больше нуля, второй меньше нуля, а третий как всегда положителен. Отрицательный множитель помноженный на положительные множители даст в итоге отрицательное число.
Первый множитель будет больше нуля, второй меньше нуля, а третий как всегда положителен. Отрицательный множитель помноженный на положительные множители даст в итоге отрицательное число.
3)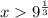
Первый множитель будет положителен, второй тоже положителен. А третий как всегда положителен. Значит в итоге, перемножив три положительных числа, получим положительное число.
В ответе получим два промежутка из первого и третьего случаев.
Заметно, что целочисленных решений будет бесконечно много. Это и все отрицательные целые числа и целые числа большие 2. Так как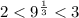
Решений, так сказать, счетное множество.
Ну, а если бы был бы в неравенстве противоположный знак, то было бы всего два решения из второго случая. Это числа 1 и 2.