Значение функции может принимать максимальное или минимальное значение в точках касания, когда касательная параллельна оси ОХ, т.е. угловой коэффициент этой прямой равен 0, т.к.tg0=0 значит ], решаем квадратное уравнение:
Корни:x=-20/3=-6,(6), он не подходит т.к. x может принимать значения от -5 до 8,
2-ой корень x=-4, подставим это значение в начальную функцию: и получим y=2, теперь подставим -5 и 8:
Шестиугольник можно разбить на 6 равносторонних треугольников, ромб - на два. Пусть сторона исходного равностороннего треугольника равна `a`. Из трех таких треугольников нужно собрать один, и его сторона тогда должна быть равна a * sqrt(3), чтобы площадь была одна и та же. Заметим, что половина стороны большого треугольника равна a * sqrt(3) / 2, а это равно высоте маленького треугольника. Разделим маленький на две части пополам, а большой - на 6 частей медианами. Части маленького и большого треугольников равны между собой.
Найдем производную функции
Значение функции может принимать максимальное или минимальное значение в точках касания, когда касательная параллельна оси ОХ, т.е. угловой коэффициент этой прямой равен 0, т.к.tg0=0 значит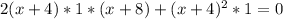
], решаем квадратное уравнение:
Корни:x=-20/3=-6,(6), он не подходит т.к. x может принимать значения от -5 до 8,
2-ой корень x=-4, подставим это значение в начальную функцию: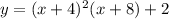
и получим y=2, теперь подставим -5 и 8:
x=-5,y=5
x=8,y=2306, т.е. наименьшее значение функции y=2
ответ: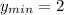
И график в доказательство
Шестиугольник можно разбить на 6 равносторонних треугольников, ромб - на два.
Пусть сторона исходного равностороннего треугольника равна `a`. Из трех таких треугольников нужно собрать один, и его сторона тогда должна быть равна a * sqrt(3), чтобы площадь была одна и та же. Заметим, что половина стороны большого треугольника равна
a * sqrt(3) / 2,
а это равно высоте маленького треугольника. Разделим маленький на две части пополам, а большой - на 6 частей медианами. Части маленького и большого треугольников равны между собой.