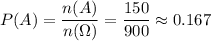- задача. По рисункам: а) определите знак углового коэффициента; в) Определите угловой коэффициент и задайте функцию по формуле

1) 36^3 + 63^3 делится на 11

Раскладываем по формуле и получаем:

(36+63)*(36^2+36*63+63^2)

(36+63) делится на 11 , следовательно 36^3 + 63^3 делитсяна 11

2) 57^3 -27^3 делится на 30

Раскладываем по формуле и получаем:

(57-27)*(57^2-57*27+27^2)

(57-27) делится на 30, следовательно 57^3 -27^3 делится на 30

3) Докажите, что 87^3 -42^3 делится на 15

Раскладываем по формуле и получаем:

(87-42)*(87^2-87*42+42^2)

(87-42) делится на 15, следовательно 87^3 -42^3 делится на 15

4) Докажите, что 23^3 + 32^3 делится на 55

Раскладываем по формуле и получаем:

(23+32)*(23^2+32*23+32^2)

(23+32) делится на 55, следовательно 23^3 + 32^3 делится на 55

Всего трехзначных чисел: 999 - 99 = 900 из них выбираем числа, которые делятся на 6.

Наименьшее число, делящееся на 6: 102, а наибольшее — 996

Последовательность чисел делящихся на 6 такова: 102; 108; .... ; 996 - арифметическая прогрессия (каждый член прибавляется число 6)

По формуле n—го члена арифметической прогрессии вычислим количество трехзначных чисел, делящихся на 6

A — Вася выбирает наугад трехзначное число.

Количество всевозможных исходов: n(Ω) = 900

Количество благоприятных исходов: n(A) = 150

По формуле классической вероятности: