Задание 1 Постройте график функции y =(x – 3)2 + 4. Задание 2 Вершина параболы – точка T(3; 3). Найди значение a, если график функции проходит через точку (1; 5).
Задание 3 Построить в одной системе координат графики функций
у=2х2, у= 2(х-5)2+3, у=-2(х+4)2-5
Задание 4 Вершина параболы – точка T(–2; 5). Найди уравнение параболы, если график функции проходит через точку A(–3; 7).
Задание 5 Как можно получить график функции y = (x – 10)2 + 17 из графика функции y = x2? Постройте график функции

ответ:(0,5x+1,6y)²=0.25x^2+2*0.5*1.6xy+2.56y^2=0.25x^2+1.6xy+2.56y^2Объяснение:Для того, чтобы представить квадрат двучлена (0,5x+1,6y)²​ в виде многочлена мы вспомним и применим формулу сокращенного умножения квадрат суммы. Квадрат суммы двух выражений (чисел) равен квадрату первого выражения (числа), плюс квадрат второго выражения (числа), плюс удвоенное произведение первого на второе выражение (число). (a + b)2 = a2 + 2ab + b2. Применим формулу и получим выражение:(0,5x+1,6y)²​=0.25x^2+2*0.5*1.6xy+2.56y^2=0.25x^2+1.6xy+2.56y^2

Исследовать на сходимость ряд    

Следовательно,     положительный  числовой ряд.

2) Чтобы ряд сходился, необходимо  (но не достаточно), чтобы его общий член стремился к нулю :

3) Интегральный признак Коши :

 Если несобственный интеграл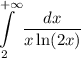    сходится (в результате вычислений получится число), то будет сходиться числовой ряд   .

 Если несобственный интеграл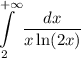    расходится (в результате вычислений получится бесконечность), то будет расходиться числовой ряд   .

4) Подынтегральная функция непрерывна на интервале [2;+∞).

ответ : ряд расходится